Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 6.Problemas - Ex. 105
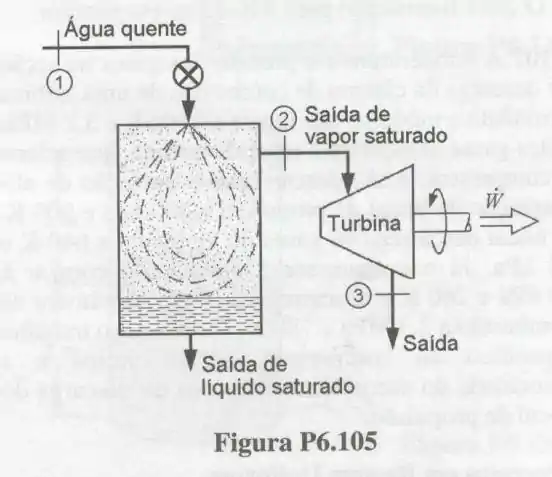
105- Propõe-se usar um suprimento geotérmico de água quente para acionar uma turbina a vapor d’água utilizando o dispositivo esquematizado na . Água a alta pressão, e , é estrangulada, num evaporador instantâneo adiabático, de modo a obter líquido e vapor a pressão de . O líquido sai pela parte inferior do evaporador, enquanto o vapor é retirado para alimentar a turbina.
O vapor sai da turbina a e com título igual a . Sabendo que a turbina produz uma potência de , qual é a vazão necessária de água quente, em , que deve ser fornecida pela fonte geotérmica?
Passo 1
Você já pensou em acionar uma turbina com energia geotérmica? Pois é nesse planeta maravilhoso tudo é possível basta só um pouquinho de vontade.
Vamos anotar o estado da água nos três pontos:
Potência da turbina: e pede-se a vazão pela fonte geotérmica, parecem dados muito difusos e diferentes né. Mas vamos com calma que resolveremos aos poucos.
Bem, no ponto a água sai a vapor (como se espera pela figura) e pela tabela para teremos as seguintes entalpias de saturação e de vapor:
E a entalpia em estado saturado a seria (pela tabela ), já que o estrangulamento por si só não é capaz de mudar a temperatura da água.
O que nos dá uma titulação de:
Como a água no ponto tem o mesmo volume no ponto sendo a diferença que no estado 2 ela está um tanto evaporada então podemos dizer:
Ou ainda melhor:
Uma vez que ela está sendo escoada.
Passo 2
Agora vamos para o ponto onde temos a saída da turbina a e com titulação de então pela tabela teremos:
Então a entalpia de água saturada no final do ponto é de:
A diferença dessa entalpia é que aqui não temos a temperatura do fluído
Passo 3
Isso é importante pois agora somos capazes de calcular a vazão que passa pela turbina pela sua potência ao fazer:
Onde pela tabela vale
Agora podemos calcular a vazão fornecida pela fonte pelo que achamos no passo 1 fazendo:
Então:
Porém se quer essa vazão por hora e não por segundo então:
E com isso chegamos ao fim de mais uma questão, espero que tenha ficado claro a questão das entalpias pois a entalpia total é sempre a do fluído saturado e com isso e com os auxílios das tabelas podemos ir encontrando as medidas corretas.