Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 6.Problemas - Ex. 116
116- Inicialmente, um conjunto cilindro-pistão, que opera a pressão constante, contém de água a e .
Existe no conjunto cilindro-pistão uma válvula que pode descarregar a água contida no conjunto na atmosfera ), Esta válvula é aberta e só é fechada quando a massa contida no conjunto se torna igual a .
Admitindo que o processo é adiabático, que a temperatura da água é sempre uniforme, determine a velocidade de descarga da água e o trabalho realizado no processo.
Passo 1
Dica de saúde: toda vez que você ver uma questão que use água nesse livro, beba um copo de água
Principalmente se tiver muito calor
Então indo para a questão, temos o estado inicial dessa água nesse conjunto
Pela tabela (já que a temperatura é muito baixa para termos dois estados), temos as seguintes propriedades
E é isso que podemos dizer sobre o estado inicial da água no conjunto
Passo 2
Agora para temos dois eventos ocorrendo de água saindo pela e uma parcela que fica no tanque com alguma energia.
Se preocupando com a parcela de água que sai do tanque.
Como de água fica no tanque e antes tínhamos de água no tanque então é seguro dizer que de água saindo do tanque.
E como a água se mantém a em todo os processos então seguramente podemos dizer que o estado dessa água é o mesmo que a do passo anterior (pois a água não consegue vaporizar)
Passo 3
Agora para a água que fica no tanque:
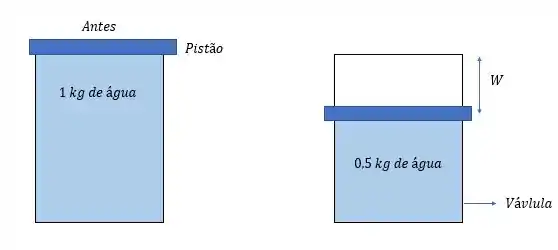
A temperatura inda se mantém de , então as propriedades da água ainda continuam sendo a mesma, somente o volume que diminuiu, logo temos um trabalho de:
Então o trabalho nesse pistão será de:
Passo 4
Agora a parte da velocidade da água na válvula. Modelando a energia nesse sistema nós teremos:
Resumindo, toda a energia interna que tínhamos na água inicialmente é transformada em trabalho por parte do pistão, acrescida da energia interna no estado final da água dentro do tanque e a energia que tem na água que sai pela válvula que é composta pela entalpia dessa água pela soma da cinética dessa água que essa água ganha
Substituindo os valores temos:
Então a velocidade da água será de:
Não esqueça de multiplicar por as medidas de e pois eles estão em .
Acabaste a questão e agora beba a sua água caso não tenha bebido ainda
