Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 12.Problemas - Ex. 2

Se a Eq. (12.1) é válida para o ELV isotérmico em um sistema binário, mostre que:

d P d x 1 x 1 = 0 ≥ - P 2 s a t d P d x 1 x 1 = 1 ≤ P 1 s a t  

Passo 1

CONHECIDO: A análise molar de uma armação de gás é especificada.

ENCONTRADO: Determinar a análise em termos de frações, a pressão parcial de cada componente e o volume gerado por 10 kg de mistura.

ESQUEMA I DADOS FORNECIDOS:

PREMISSAS. (1) A mistura geral atua como um gás ideal. (2) Cada componente da mistura se forma como se fosse um gás ideal ocupando todo o volume na temperatura de névoa. (3) Os cálculos são baseados em i kmol de mistura .

ANÁLISE (A) Considerando um típico 1 kmol de mistura

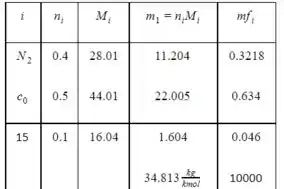
Passo 2

(b) com Eq 12.12

P N 2 = y N 2 P = ( 0.4 ) ( 2   b a r   ) = 0.8   b a r

P c ∘ 2 = y c ∘ 2 p = ( 0.5 ) ( 2 b a r ) = 1.0 b a r

P c l m = y c ∘ 2 = ( 0.1 ) ( 2 b a r ) = 0.2 b a r

Passo 3

(c) Com a equação de estado ideal dos gases aplicada à mistura geral.

V = m ( R _ / M ) T P

= ( 10 k g ) 83.4 34.813 N ⋅ m k g ⋅ k ( 303 k ) 2 × 10 5 N / m 2 = 3.618 m 3

O peso molecular aparente da mistura é obtido nos cálculos da parte (a). Equivalentemente M = ∑ y i M i

M = y N 2 M N 2 + y C O 2 M C Q 2 + y 14 M L H 4

= ( 0.4 ) ( 28,06 ) + ( 0.5 ) ( 44.01 ) + ( 0.1 ) ( 16.04 ) = 34.813 k g k m o l

Resposta

34.813 k g k m o l

Ver Outros Exercícios desse livro