Uma mistura bifásica líquido-vapor de H2O, inicialmente com x = 30% e uma pressão de 100 kPa, está contida em um conjunto cilindro- pistão, como ilustrado na Fig. P3.77. A massa do pistão é de 10 kg, e ele possui 15 cm de diâmetro. A pressão da vizinhança é de 100 kPa. À medida que a água é aquecida a pressão no interior do cilindro permanece constante até que o pistão atinge os esbarros. A transferência de calor para a água continua, a volume constante, até que a pressão atinja 150 kPa. O atrito entre o pistão e as paredes do cilindro e os efeitos das energias cinética e potencial são desprezíveis. Para o processo global relativo à água, determine o trabalho e o calor transferido, ambos em kJ.
Passo 1
Ooopa, beleza?
Vamos lá pra mais uma questão bem interessante de termodinâmica!
Passo 2
O diagrama é mostrado abaixo
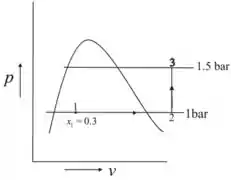
Passo 3
O processo 1-2 tem pressão constante, calculando o trabalho feito usando a equação
Durante o processo 2-3, o volume permanece constante, então o trabalho é zero
Passo 4
Calculando o volume da mistura líquido-vapor no estado 1
Calculando o volume do vapor no estado 2
Passo 5
No estado 1, o sistema é líquido-vapor a uma pressão de . Da Tabela A-3 “Propriedades de Água Saturada – Tabela de Pressão”
Calculando o volume específico no estado 1
Calculando a massa da mistura no sistema
Calculando a energia interna específica no estado 1
Durante o processo 2-3 o volume permanece constante
Passo 6
Calculando o trabalho feito durante o processo 1-2 usando
Passo 7
Calculando a energia interna específica no estado 3 ( e ) da Tabela A-4 “Propriedades de Vapor de Água Superaquecido” interpolando a temperatura entre e
Aplicando o balanço de energia para o sistema