Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 128
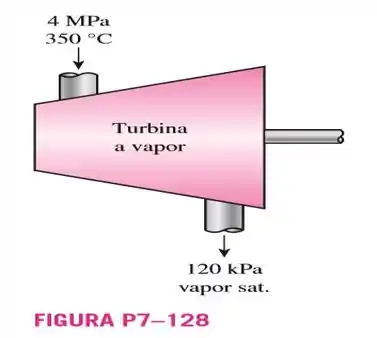
128. Vapor a e é expandido em uma turbina adiabática até . Qual é a eficiência isentrópica da turbina, considerando que o vapor é expelido como vapor saturado?
Passo 1
Olha só! Inicialmente, para se resolver esse problema, vamos destacar alguns pontos importantes que podemos perceber em nosso enunciado...
A primeira coisa perceptível, é que este nosso processo, é um processo de fluxo constante pois não há alterações significativas com o tempo.
A segunda coisa importante, é que alterações decorrentes dos efeitos de energia cinética e potencial, são desprezíveis.
A terceira, é que a turbina é adiabática, e portanto a transferência de calor é insignificante.
Passo 2
Terminada essa parte introdutória, que é chatinha, mas extremamente importante bora por a mão na massa de verdade.
Olha só! Espera-se que exista apenas uma entrada e apenas uma saída em nosso sistema. Sendo assim...
Tomamos a turbina como sistema, que é um volume de controle, uma vez que a massa atravessa a fronteira. Observando que uma corrente de fluido entra e sai do compressor, o balanço de energia para este sistema de fluxo constante pode ser expresso na forma de taxa como...
Como a nossa compressão ocorre em regime permanente...
E ficamos com...
Como valor é expelido como ar saturado, espera-se que seja gerada uma potência de saída, uma potência que é real. Sendo assim
Só que...
O que nos faz ficar com...
Passo 3
Onde das tabelas e , tiramos os seguintes valores...
Feito isso, para obter a eficiência isentrópica da turbina basta dividir a potência real pela potência isentrópica na saída:
Pronto! Resposta obtida!