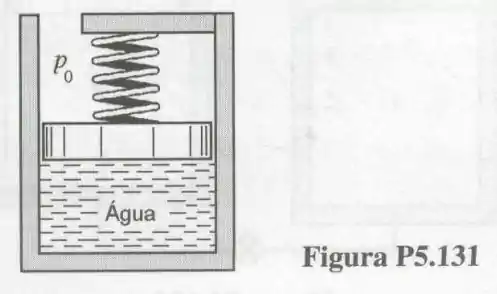
131- O conjunto cilindro-pistão-mola linear mostrado na contém água, a e , e apresenta volume interno igual a . Se o pistão estiver encostado no fundo do cilindro, a mola toca o pistão, mas não exerce força sobre ele e a pressão interna necessária para movimentar o pistão, nesta condição, é . Calor é transferido do sistema até que a pressão atinja . Determine o calor transferido no processo.

Agora para o estado cuja pressão e só essa é a única informação de estado que temos só que aí que vem a sacada.

Saca, quando vamos na tabela e vamos procurar quanto vale uma informação da água a mas só tem informação de e ? Aí fazemos uma projeção linear da coisa para achar justamente quando a situação aperta.

Então aqui não é diferente, vamos tratar as informações como lineares, ou seja

Pois as três pressões são lineares entre si

Onde pois é o mínimo de pressão que precisa para movimentar a mola e basta não ter nenhuma água para isso. Logo:

Para esse volume específico na tabela teremos para água saturada a , pegar dessa tabela é necessária pois não sabemos sua temperatura

Portanto a titulação nesse estado será:

Portanto a energia interna nesse estado será:

Agora para calcular o calor falta o trabalho que é feito com:

E como tanto pressão quanto volume variam de forma linear então a fórmula para calcular esse trabalho será da forma:

Falta somente o volume final, e que será dado por:

Portanto o trabalho será de:

Então para fechar o tanto de calor fornecido será de:

Questão braba demais, vamos para mais dessas!