138- Ar a e escoa sobre uma placa de aço que apresenta temperatura superficial constante e igual a . O escoamento é tal que proporciona um coeficiente de transferência de calor por convecção igual a . Sabendo que a vazão de ar é igual a e que o ar só transfere calor para a placa, determine a área da placa necessária para que a temperatura do ar seja reduzida a . Qual é a área da placa necessária para que o ar atinja ?

Convecção nossa que estais nas nossas vidas, santificada seja vosso Nome, venha aquecer nossas vidas de acordo com nossa vontade assim na terra como no Céu.

Primeiro ele quer que esse ar que está a (que é bastante coisa a beça) diminua para . Primeiro a transferência de calor desse ar sabendo que:

Pela tabela a entalpia do ar a é de e do ar a é de , então o calor para uma vazão mássica de será:

E como a temperatura da placa tem que estar a então a taxa de calor por convecção será:

Agora vem o pulo do gato se liga na figura abaixo

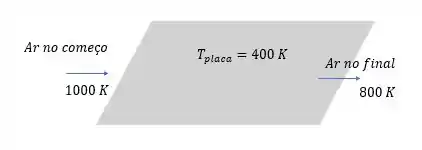
Supondo que o ar escoa rente a placa e diminua de temperatura linearmente a medida que passa pela placa, então a variação de temperatura no começo será:

Agora a variação de temperatura no final:

Como estamos falando de um escoamento e não um ponto fixo então podemos dizer que em média a diferença de temperatura do ar e da placa tem uma média de enquanto passa pela placa ok?

Dessa forma a transferência de calor será:

Nos dando uma área de: