Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 147
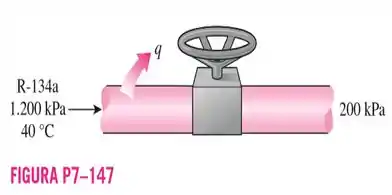
147. Refrigerante- inicialmente a e é estrangulado até . O refrigerante perde calor a uma taxa de para a vizinhança, que está a . Determine (a) a temperatura de saída do refrigerante e (b) a geração de entropia durante esse processo.
Passo 1
Olha só! Inicialmente, para se resolver esse problema, vamos destacar alguns pontos importantes que podemos perceber em nosso enunciado...
A primeira coisa perceptível, é que em nosso sistema, existem condições operacionais estáveis.
A segunda coisa importante, é que a influência das energia cinética e potencial em nosso problema, serão consideradas desprezíveis.
Passo 2
Terminada essa parte introdutória, que é chatinha, mas extremamente importante bora por a mão na massa de verdade.
As propriedades do refrigerante na entrada do dispositivo, de acordo com a tabela , são:
Já a entalpia do refrigerante na saída do dispositivo, vai ser dada por...
Onde esse é a taxa de calor perdido pelo refrigerante...
a)
Em seguida, usando a tabela , vamos obter as propriedades do refrigerante no estado de saída...
Pronto! Já obtemos a temperatura do refrigerante.
Passo 3
A geração de entropia associada a esse processo pode ser obtida adicionando a alteração de entropia do à medida que flui no dispositivo e a alteração de entropia dos arredores
Dito isso, vamos expressar o balanço de entropia para este sistema de fluxo constante como...
Como existem condições operacionais estáveis, então...
E ficamos com...
Só que como temos uma única entrada e saída no sistema, então...
E também temos que...
Ou seja...
Trabalhando com entropia por unidade de massa no tempo, ficamos com...
Passo 4
Fazendo o cálculo para o :
E depois para a outra parte...
E desse modo, substituindo os valores numéricos obtidos acima na última fórmula do , a geração de entropia vai ser igual à...