Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 2.Problemas - Ex. 73

A mostra dois conjuntos cilindro - pistão conectados por uma tubulação. Os conjuntos A e B contém um gás e as áreas das seções transversais são respectivamente iguais a . A massa do pistão do conjunto A é igual a , a pressão ambiente é e o valor da aceleração da gravidade é o normal. Calcule, nestas condições, a massa do pistão do conjunto B de modo que nenhum dos pistões fique apoiado nas superfícies inferiores dos cilindros.

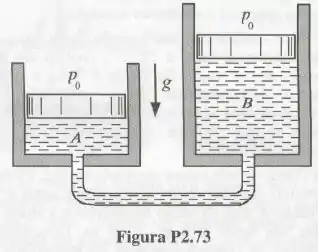
Passo 1

Oi pessoal, tudo certo? Vamos analisar essa questão!

Aqui temos um típico exercício de balanço de pressões. Como o exercício não nos deu a diferença de altura do fluido, podemos considerar que o sistema está em equilíbrio. Portanto:

Como as únicas pressões agindo nos tanques são as pressões atmosféricas e devido ao peso dos pistões, temos que:

Simplificando, temos que:

Agora é só calcular:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Agua doce e agua do mar escoam em tubulações horizontais paralelas e estão conectadas entre si por um manômetro de tubo em U duplo, como mostra a Figura. Determine a diferença de pressão entre as duas

Repita o Prob. 1–78 substituindo o ar por óleo, cuja densidade relativa e de 0,72.

Considere o manômetro na figura. Se o peso especifico do fluido A e 100k N / m 3 , qual e a pressão absoluta, emk P a , indicada pelo manômetro quando a pressão atmosférica local e de. 90k P a ?

Considere o manômetro na figura. Se o peso especifico do fluido B e 12 k N / m 3 , qual e a pressão absoluta (em k P a ) indicada pelo manômetro quando a pressão atmosférica local e de. 720 m m

Calcule a pressão absoluta, P 1 , do manometro mostrado na figura em k P a . A pressao atmosferica local e 758 m m H g .