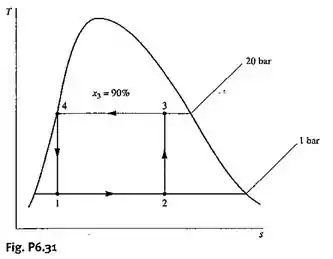
31. A Fig. P6.31 fornece o diagrama T-s de um ciclo de bomba de calor de Carnot para o qual a substância é a amônia. Determine o trabalho líquido de entrada necessário, em kJ, para 50 ciclos de operação em 0,1 kg de substância.
Passo 1
Aqui temos um processo de refrigeração por um ciclo de bomba de Carnot, composto pelos processos:
-Processo 1-2: Compressão isotérmica (T1=T2);
-Processo 2-3: Compressão adiabática (Q23=0) de T2 até T3;
-Processo 3-4: Expansão isotérmica (T3=T4);
-Processo 4-1: Expansão adiabática (Q41=0) de T4 até T1;
Vamos relembrar que para um Ciclo de Carnot, os processos ocorrem de forma reversível, assim quando se fala que o processo é adiabático, ele quer dizer também que o mesmo é isentrópico, e isentrópico quer dizer que a entropia não varia de um estado a outro.
Então,
-No processo 2-3:
-No processo 4-1:
Passo 2
Para a resolução do problema, é válido estabelecer as considerações acerca do processo.
As considerações que podem ser feitas são:
-Regime permanente (sem variação das propriedades com o tempo);
-Variações de energia cinética e potencial desprezíveis;
Passo 3
O que foi pedido no problema é o trabalho líquido de entrada, sendo que este trabalho de entrada significa o trabalho do compressor, ou seja, o trabalho do sistema de compressão, que está fornecendo energia ao sistema. Assim, vamos precisar encontrar o trabalho do compressor para um ciclo.
Pelas descrições dos processos, a compressão ocorre no processo 2-3, a compressão adiabática.
Vamos fazer um balanço de energia no processo 2-3 para chegar numa expressão para o trabalho 2-3, W23
A equação do balanço de energia é
Onde,
-m é a massa do fluido (amônia);
-, é a variação de energia total, em que essa energia total é a soma da energia interna (U), energia cinética (EK) e energia potencial (EP);
-, é a energia interna especifica;
-, é a energia cinética especifica;
-, é a energia potencial especifica;
-Q é o calor transferido;
-W é o trabalho.
Como foi considerado que as variações de energia cinética e potencial são desprezíveis, logo você pode eliminar elas da equação
Vamos agora aplicar essa equação ao processo 2-3
O processo 2-3 ocorre de forma adiabática, então Q23=0
Já temos a massa, mas não temos as energias internas especificas e .
Passo 4
Para achar as energias internas vamos analisar o diagrama T-S do enunciado e usar os dados fornecidos.
Você vai ver que no ponto 3 (estado 3), temos a pressão p3=20 bar e o título, x3=90%=0,90, vamos então usar estes valores para determinar .
Pela definição de título
Onde,
-x3 é o título no estado 3;
-, é a energia interna especifica do líquido saturado;
-, é a energia interna especifica do vapor saturado;
Os valores para , , são encontrados diretamente na tabela de dados para a amônia saturada na pressão p3=20bar.
Pela Tabela A-14 do livro Shapiro-Princípios da Termodinâmica, 7ª Edição:
Calculando
Passo 5
Também pelo diagrama T-S, você vai ver que o ponto 2 (estado 2) se encontra dentro da região bifásica e você vai precisar então de outros dois dados para encontrar .
Nesse estado, já temos a pressão p2=1,0 bar. Outro dado que você pode usar é o título do estado 2, x2, na qual você consegue calcular pela entropia S2 que é igual a entropia do estado 3, S3, sendo que S3 você pode achar na mesma tabela A-14, da mesma forma que você achou
Analogamente,
Onde,
-, é a entropia especifica do estado 3;
-, é a entropia especifica do líquido saturado;
-, é a entropia especifica do vapor saturado;
Pela Tabela A-14 do livro Shapiro-Princípios da Termodinâmica, 7ª Edição, na pressão de 20 bar:
Calculando
E
Para o título no estado 2
Aqui as entropias especificas e devem ser determinadas na pressão de 1,0 bar.
Pela Tabela A-14 do livro Shapiro-Princípios da Termodinâmica, 7ª Edição, na pressão de 1,0 bar:
Substituindo os valores
Para
Aqui as energias interna especificas e também devem ser determinadas na pressão de 1,0 bar.
Pela Tabela A-14 do livro Shapiro-Princípios da Termodinâmica, 7ª Edição, na pressão de 1,0 bar:
Calculando
Passo 6
Agora para finalizar, é só aplicar os valores encontrados
Aplicando os valores
Este valor achado foi para um ciclo, então para 50 ciclos, o trabalho total é
O sinal negativo representa que a energia está sendo consumida pelo sistema.