34. Um ciclo de potência de Carnot opera em regime permanente conforme ilustrado na Fig. 5.15, com água como fluido de trabalho. A pressão da caldeira é de 200 lbf/in2 (1,4 MPa), sendo que o fluido de trabalho entra como líquido saturado e sai como vapor saturado. A pressão do condensador é de 20 lbf/in2 (137,9 kPa).
A) Esboce o ciclo em coordenadas T-s.
B) Determine a quantidade de calor transferida e o trabalho para cada processo, Btu por lb de água escoando.
C) Avalie a eficiência térmica
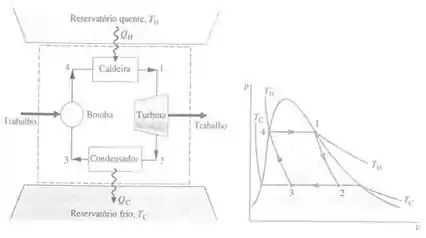
Fig. 5.15
Passo 1
A)
Aqui temos um processo de geração de potência composto pelos equipamentos: Bomba, Caldeira, Turbina a vapor e Condensador, tendo a água como fluido de trabalho, onde ela irá escoar pelos equipamentos mencionados e ocorrerá a geração de potência.
Para este processo, com um ciclo de potência de Carnot, o diagrama que descreve o ciclo é dado pelo seguinte diagrama:
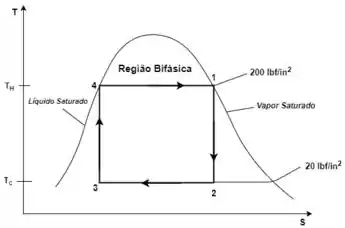
O ciclo de Carnot é dado pelos processos 1-2, 2-3, 3-4 e 4-1, do diagrama T-S. Você pode descrever cada processo para saber o que acontece em cada etapa.
-Processo 1-2: Expansão isentrópica (entropia constante) do vapor de água na turbina de p1 até p2;
-Processo 2-3: Condensação da água no condensador a pressão constante;
-Processo 3-4: Bombeamento isentrópico (entropia constante) da água, fazendo uma compressão de p3 até p4;
-Processo 4-1: Geração de vapor de água na caldeira a pressão constante;
Passo 2
Para a resolução do problema, é válido estabelecer as considerações acerca do processo.
As considerações que podem ser feitas são:
-Regime permanente (sem variação das propriedades com o tempo);
-Sistema aberto, pois há escoamento de fluido;
-Turbina e bomba operando isentropicamente (sem variação de entropia, sem transferência de calor, Q=0 para a turbina e a bomba);
-Variações de energia cinética e potencial desprezíveis;
Passo 3
B)
Primeiramente, vamos modelar as equações para cada equipamento que serão usadas para os cálculos do trabalho e do calor transferido.
Na modelagem para cada equipamento você vai aplicar o balanço de energia para sistemas abertos, ou seja, o balanço de energia considerando o escoamento do fluido, com entradas e saídas, cuja expressão é
Onde,
- é a taxa de variação de energia interna do volume de controle, ou seja, é a quantidade de energia interna do volume de controle (UVC) que varia ao longo do tempo;
-, é taxa de transferência de calor, em unidades de kJ/s;
-, é a taxa de transferência de trabalho, em unidades de kJ/s;
-, é vazão mássica do processo;
-, é variação de entalpia especifica, sendo essa entalpia especifica a entalpia dividida por unidade de massa, em unidades de kJ/kg;
-, é a variação de energia cinética específica, em unidades de kJ/kg;
-, é a variação de energia potencial específica, em unidades de kJ/kg;
Vamos simplificar a equação do balanço de energia através das considerações.
Levando em conta as considerações feitas, o termo , se anula, pois não há variação das propriedades com o tempo e, e , também se anulam, pois foram desprezadas, tendo em vista que a variação de entalpia possui valor mais significativo do que estes.
Assim, o balanço de energia é simplificado para
Onde,
-, é entalpia especifica do fluido na saída do equipamento;
-, é entalpia especifica do fluido na entrada do equipamento;
Então, essa é a expressão do balanço de energia que você vai usar na modelagem de cada processo.
As entalpias especificas você vai determinar a partir de tabelas de dados termodinâmicos.
Passo 4
-Processo 1-2: Turbina
Como foi considerado que a turbina opera isentropicamente, isso quer dizer que não há variação de entropia na turbina, então S1=S2.
Assim, para você achar o calor transferido nessa etapa, você pode usar a relação matemática entre calor e variação de entropia, que é a seguinte
Assim, o calor se anula, pois não a variação de entropia especifica
Pelo balanço de energia
Onde,
-, é a energia interna especifica no estado 2 (saída da turbina);
-, é a energia interna especifica no estado 1 (entrada da turbina);
Como
Veja que temos a vazão mássica que não foi fornecido no problema, mas foi pedido o trabalho em Btu/lb, isto é, em unidades de energia por unidade de massa, então o que você vai precisar fazer é dividir o termo do trabalho pelo termo da vazão mássica, ficando a equação dessa forma
Passo 5
-Processo 2-3: Condensador
O condensador é um equipamento em que não há trabalho sendo exercido sobre o fluido, então o trabalho nessa etapa é nulo
Pelo balanço de energia
Onde,
-, é a energia interna especifica no estado 2 (entrada do condensador);
-, é a energia interna especifica no estado 3 (saída do condensador);
Como
Passo 6
-Processo 3-4: Bomba
Assim como para a turbina, foi considerado que a bomba opera isentropicamente, então S3=S4.
Da mesma forma,
Assim, o calor se anula, pois não a variação de entropia especifica
Pelo balanço de energia
Onde,
-, é a energia interna especifica no estado 4 (saída da bomba);
-, é a energia interna especifica no estado 3 (entrada da bomba);
Como
Passo 7
-Processo 4-1: Caldeira
Assim como no condensador, a caldeira é um equipamento em que não há trabalho sendo exercido sobre o fluido, então o trabalho nessa etapa também é nulo
Pelo balanço de energia
Onde,
-, é a energia interna especifica no estado 4 (entrada da caldeira);
-, é a energia interna especifica no estado 1 (saída da caldeira);
Como
Passo 8
Encontrando os valores das entalpias especificas em tabela:
Olhando lá no diagrama T-S, você vai ver que os pontos 4 e 1 (estados 4 e 1, respectivamente) se encontram em cima da curva. Quando um ponto está em cima da curva, significa que o fluido está como líquido saturado ou vapor saturado. Se você olhar no diagrama vai ver que o ponto 4 é de liquido saturado e o ponto 1 é de vapor saturado.
Então, para você achar as entalpias nesses estados, é só você ir em uma tabela de dados para água saturada, usando a pressão de 200 lbf/in2.
Pela Tabela A-4E do livro Shapiro-Princípios da Termodinâmica, 7ª Edição:
Também pelo diagrama T-S, você vai ver que os pontos 2 e 3 (estados 2 e 3, respectivamente) se encontram dentro da região bifásica, assim a água é uma mistura de líquido e vapor e você vai precisar então de outros dois dados para encontrar e .
Sempre quando você for precisar de encontrar um valor de uma propriedade quando o fluido é uma mistura líquido vapor, você pode usar o título pegando a sua definição
Onde,
-x3 é o título no estado 3;
-x2 é o título no estado 2;
-, é a energia interna especifica do líquido saturado;
-, é a energia interna especifica do vapor saturado;
No enunciado não foi fornecido o valor para o título, mas você pode calcula-lo, relacionando-o com a entropia especifica
Onde,
-, é a entropia especifica do estado 2;
-, é a entropia especifica do estado 3;
-, é a entropia especifica do líquido saturado;
-, é a entropia especifica do vapor saturado;
Pelo diagrama você vai ver que
Então o que você precisa fazer é achar a entropia especifica do estado 1 (vapor saturado) e 4 (liquido saturado) e é só você ir em uma tabela de dados para água saturada, usando a pressão de 200 lbf/in2.
Pela Tabela A-4E do livro Shapiro-Princípios da Termodinâmica, 7ª Edição:
Os valores para , , , , são encontrados diretamente na tabela de dados para a água saturada na pressão de 20 lbf/in2.
Pela Tabela A-4E do livro Shapiro-Princípios da Termodinâmica, 7ª Edição:
Calculando x3 e x2:
Calculando e :
Passo 9
Agora com as entalpias determinadas é só aplicar os valores para calcular a taxa de trabalho e a taxa de transferência de calor em cada processo
-Processo 1-2:
-Processo 2-3:
-Processo 3-4:
-Processo 4-1:
Passo 10
C)
Calculando e eficiência térmica:
A eficiência térmica, ηT, em um processo de ciclo de potência representa o quanto de energia disponível foi usado para gerar trabalho útil. Então, você pode calcular seu valor pela seguinte expressão
Onde,
-, é a taxa de transferência de calor que é fornecido ao processo, sendo fornecido pela caldeira, ;
-, é a taxa de transferência de trabalho líquido do ciclo sendo a diferença entre a taxa de trabalho da turbina, , e a taxa de trabalho da bomba, .
Então,
Substituindo os valores,
Resposta
B)
-Processo 1-2:
-Processo 2-3:
-Processo 3-4:
-Processo 4-1:
C)