Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 12.Problemas - Ex. 66
66- Uma turbina é alimentada com de uma mistura composta por de hélio e de nitrogênio (base mássica).
A pressão e a temperatura na seção de alimentação da turbina são respectivamente iguais a e e a pressão na seção de descarga do equipamento é .
Sabendo que a eficiência isoentrópica do equipamento é igual a , determine a potência gerada na turbina.
Passo 1
Fala pessoal! Tudo bem com vocês? Pega um café e vamos para essa questão
Antes de falar de isenção isoentrópica e a coisas relacionadas a questão vamos por em um desenho tudo que está sendo falado no enunciado
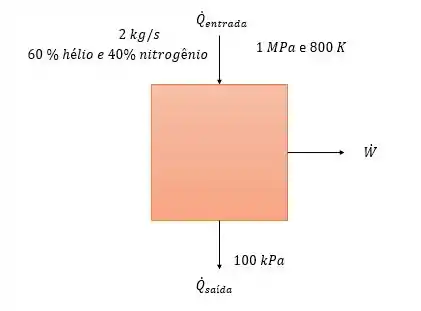
Como temos gases nobres e não temos acesso a suas entalpias, então vamos pegar suas constantes
E como temos uma proporção de de hélio e de de nitrogênio na mistura, então
Eu sempre gosto de pegar essas propriedades antes pois podemos usar elas sempre que precisarmos
Passo 2
Agora vamos para a questão de fato, o que ele quer de nós nessa hora tão bela? Bem, ele quer a potência dessa turbina, bem a potência nós sabemos calcular e ela vale:
Aí poderíamos fazer a aproximação que , mas aí veríamos que nos falta a temperatura na descarga (saída), e nessa hora a questão nos trai e não nos dá uma dica de como ocorre essa transformação, então vou ficar com a questão original que nos diz que
Que a turbina é adiabática, então a temperatura na sua seção de descarga será de:
Onde:
Então a temperatura na saída será de:
Passo 3
Agora estamos seguros a poder calcular a potência dessa turbina pois:
Só que temos de eficiência do motor, então:
E esses foram os passos que dei para resolver a questão, se ficou alguma dúvida nos mande sua mensagem.