Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 9.Problemas - Ex. 80

80- Uma bomba de pequeno porte é acionada por um motor que apresenta potência igual a 2   k W . A bomba é alimentada com água a 150   k P a e 10   ° C .

Determine a máxima vazão na bomba sabendo que a pressão na seção de descarga da bomba é igual a 1   M P a . Despreze as energias cinéticas dos escoamentos nas seções de alimentação e descarga da bomba. Uma mangueira com bocal de descarga está conectada a bomba.

Sabendo que a mangueira descarrega a água na atmosfera ( p a t m = 100   k P a ) e que o diâmetro da seção de saída do bocal é pequeno, determine a velocidade do jato na seção de saída do bocal.

Passo 1

E se eu te dissesse que um desenho vai te deixar apto pra resolver essa questão como num estalar de dedos?

Então lá vai

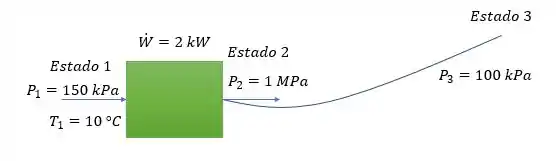
E é isso a questão valeu até a próxima!

Ko hahaha vamos encontrar o que ele quer que é a velocidade do jato na saída da mangueira (no estado 3) e a máxima vazão da bomba.

Passo 2

Pela temperatura do estado 1 tiramos o volume específico da água na tabela B . 1.1 que é de:

ν = 0.001   m 3 / k g

A vazão que ocorre na bomba é aquela que ocorre entre as pressões de 150   k P a e 1   M P a , pois são as pressões que tem na entrada e na saída da mesma

W ˙ = m ˙ ν P s á i d a - P e n t r a d a

Substituindo os valores que conhecemos teremos:

2 = m ˙ × 0.001 1000 - 150

m ˙ = 2.353   k g / s

E isso responde uma parte da questão, agora nossa missão é a velocidade da saída

Passo 3

Quando nos é dito que o diâmetro é muito pequeno, isso quer dizer que podemos considerar a saída como a atmosférica, mas mais importante é que podemos considerar a vazão única por todo o trajeto

Considerando a velocidade na seção de descarga da bomba como nula e como não temos nenhuma variação de altura na mangueira então a equação de Bernoulli fica:

m ˙ 2   v f 2 = m ˙ ν P s a í d a - P i n i c i a l

Logo a velocidade na saída da mangueira será de:

v f = 2 ν P s a í d a - P i n i c i a l

Onde estamos analisando aqui os trajetos entre 2 e 3 , pois ela que gera velocidade na água

v f = 2 × 0.001 1000 - 100 × 10 3 = 42.43   m / s

Lembre-se que a pressão é em k P a , então coloque a unidade certa.

Yay, fizemos mais uma questão, até mais

Resposta

m ˙ = 2.353   k g / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Todos sabem que a eficiência das máquinas térmicas aumenta à medida que a temperatura da fonte de energia também aumenta. Em uma tentativa para melhorar a eficiência de uma usina, alguém sugere transf
Descreva um processo imaginário que viole a primeira e a segunda leis da termodinâmica.
O que é a eficiência de segunda lei? Em que ela difere da eficiência de primeira lei?
Uma usina de potência cuja eficiência térmica é maior do que a eficiência de uma segunda usina necessariamente tem uma eficiência de segunda lei mais alta do que essa outra usina? Explique.
Um refrigerador cujo COP é maior do que o coeficiente de um segundo refrigerador tem necessariamente maior eficiência de segunda lei do que esse outro refrigerador? Explique.