Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 3.Problemas - Ex. 81
81. Um tanque rígido cujo volume é desconhecido está dividido em duas partes por uma partição. Um dos lados do tanque contém um gás ideal, a 927 °C. O outro lado está evacuado e tem um volume que equivale a duas vezes o tamanho da parte que contém o gás. A partição é então removida e o gás expande-se, preenchendo todo o tanque. Calor é transferido ao gás até que a pressão seja igual à pressão inicial. Determine a temperatura final do gás.
Passo 1
A questão quer saber quanto vale a temperatura final do gás , depois que ele se expande e ganha calor. O gás se expande e se aquece até a pressão final ficar igual à pressão inicial . A figura abaixo mostra o estado do gás antes da expansão e do aquecimento (estado 1) e depois da expansão e do aquecimento (estado 2).
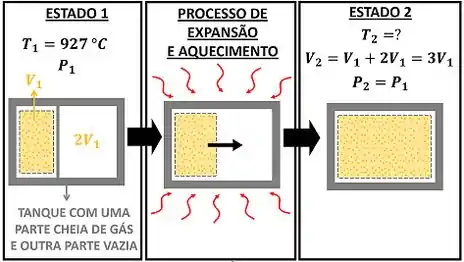
é o volume inicial que o gás ocupa e é o volume final que o gás ocupa. é a temperatura inicial do gás.
Para descobrir quanto vale , teremos que usar a equação de gás ideal para o estado 1 e para o estado 2.
onde é o número de mols de gás presente no tanque. O número de mols não muda, porque não entra gás nem sai gás do tanque durante o aquecimento e a expansão.
é a constante universal dos gases.
No próximo passo aprenderemos a usar essas equações para calculat .
Passo 2
Como e da equação de gás ideal são constantes, podemos rearranjas essas equações e criar uma relação entre elas.
Substituindo o valor de da primeira equação na segunda equação, obtemos uma nova relação.
Além disso, o enunciado diz que, ao expandir, o gás passa a ocupar o espaço vazio. Como o espaço vazio tem o dobro de volume do espaço inicial , achamos que vale:
Logo:
Lembrando que a pressão final do sistema é igual a pressão inicial , podemos cortar e da equação acima.
Substituindo os dados na fórmula de acima, conseguimos obter o valor dessa temperatura final.
Cuidado! Antes de substituir na fórmula, temos que converter de para kelvin .