83- Uma bomba d’água pequena é alimentada com água proveniente de um poço. A distância entre a superfície livre da água no poço e a bomba é .
A pressão e a temperatura da água do poço são iguais a e . A pressão na seção de descarga da bomba é . A pressão absoluta na água deve ser, no mínimo, o dobro da pressão de saturação para que não ocorra cavitação no escoamento.
Qual é o valor máximo de para que não ocorra cavitação nesta instalação?
Passo 1
Uma pesquisa feita pelo instituto de pesquisa DADOS-VERÍDICOS—E-CONFIÁVEIS-ACREDITE-EM-MIM-PFVR diz que 10 entre cada 10 aspirantes a engenheiros e 9 entre 10 engenheiros temem a palavra cavitação, pois não lembram o que isso significa.
Mas não há motivo para pânico meus alunos, pois felizmente vivemos na era da informação e podemos fazer uma leve pesquisa sobre o que é isso (ao menos que você esteja na prova, aí você não deveria estar lendo isso aqui né :P).
Cavitação é quando temos uma vaporização muito rápida em um líquido pela redução da pressão durante o movimento de uma bomba. Agora vamos para a questão pois a resolução nos aguarda.
Fazendo o esboço da questão nós temos
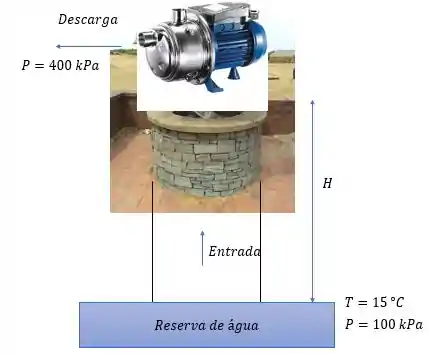
E o prêmio de edição de arte vai para o Responde Aí, eu só queria agradecer por esse prêmio você são demais ;D
Então podemos pegar as propriedades da água que está no fundo do poço na tabela
E esses dados já são suficientes para essa questão
Passo 2
Mas agora eu quero você entre no modo focado e repare umas coisas comigo
Ele nos diz que a pressão da bomba na descarga é de , ok nada a comentar, mas guarde isso no seu cerebelo.
Depois disso ele diz que
A pressão absoluta na água deve ser, no mínimo, o dobro da pressão de saturação para que não ocorra cavitação no escoamento.
Como assim? Não entendi, lembra que eu disse que a cavitação era um fenômeno da água que ocorria na bomba? Então onde a pressão deve ser o dobro da pressão de saturação da água? Na entrada da bomba meu aluno
Então a pressão na área de entrada da bomba tem ser no mínimo de:
O que nos dá a bela arte abaixo (ironia por que eu sei que tá ruim mesmo hahaha):
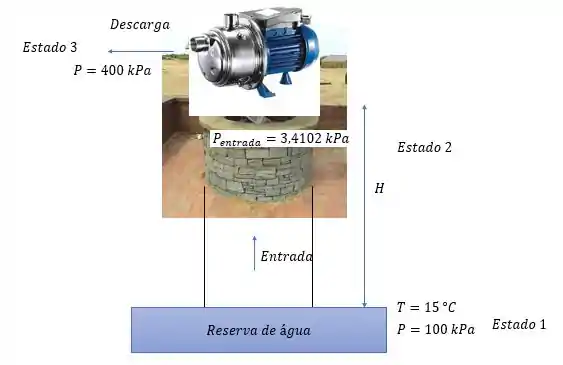
Note os estados que a água passa
Passo 3
Fazendo a equação do balanço de energia na bomba entre os estados 1 e 2 nós teremos
Para constante, ou seja a energia na água quando ela está parada com é a mesma que a potencial gravitacional no ponto de entrada da bomba somada com a energia da pressão na entrada da mesma. O que nos dá:
O que nos dá:
Sim. A pressão de no final não nos interessará em nada hahaha
Até a próxima galera!