Enunciado

Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 6.Problemas - Ex. 39

Na figura , os estados estão em uma linda de constantes

a) mostre que tanto não podem ser alcançados por processos isentrópicos a partir do estado , provando que o ciclo viola o enunciado de Kelvin-Planck da segunda lei.

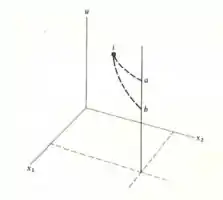
Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de termodinâmica de Sears e Salinger dada a figura abaixo onde, os estados estão em uma linda de constantes

a) mostre que tanto não podem ser alcançados por processos isentrópicos a partir do estado , provando que o ciclo viola o enunciado de Kelvin-Planck da segunda lei.

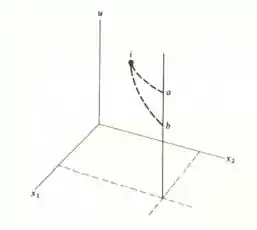
Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Passo 2

Então galerinha nessa questão ele deseja mostrar que seu processo do ciclo de Carnot apresenta o sistema com três variáveis definido como,

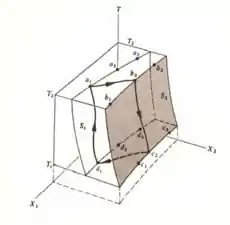
Ficando,

Sendo,

Logo podemos definir que,

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

Exercícios de Livros Relacionados

É um fato bem estabelecido que a eficiência de uma máquina térmica aumenta à medida que a temperatura T L (na qual o calor é rejeitado da máquina térmica) diminui. Em um esforço para aumentar a eficiê

Use a Figura 5.10 para mostrar que sempre que um sistema efetua um cicio fechado, a soma do fluxo de calor Q ;, dividido pela temperatura do reservatório T ; para cada processo, é menor ou igual a zer

Mostre que, se o enunciado de Kelvin-Planck da segunda lei não fosse verdadeiro, seria uma possível violação do enunciado de Clausius.

Mostre que, se o enunciado de Clausius da segunda lei não fosse verdadeiro, seria possível uma violação do enunciado de Kelvin-Planck.