Água contida em um conjunto cilindro-pistão, inicialmente à temperatura de -300°F (148,9°C), um título de 90% e um volume de 6 ft3 (0,17 m3), é aquecida a temperatura constante até o estado de vapor saturado. Considerando que a taxa de transferência de calor é de 0,3 Btu/s (0,32 kW), determine o tempo, em minutos, para que este processo da água ocorra. Os efeitos das energias cinética e potencial são desprezíveis.
Passo 1
Ooopa, beleza?
Vamos lá pra mais uma questão bem interessante de termodinâmica!
Passo 2
É dado que:
- Temperatura inicial:
- Título inicial:
- Volume inicial:
- Estado final é vapor saturado
- Taxa de transferência de calor:
- Efeitos de energia potencial e cinética são desconsideradas
Passo 3
Um desenho do processo em um diagrama
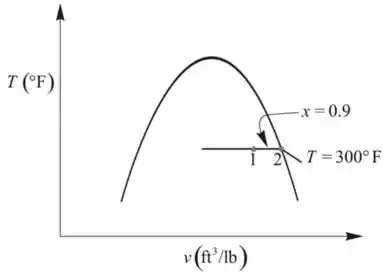
Passo 4
Para achar o tempo para esse processo ocorrer, primeiro fazemos o balanço de energia
Para achar o trabalho, usando a fórmula para expansão e compressão devido a pressão do fluido
Passo 5
Para achar o volume específico no estado 1, usando a fórmula para uma mistura bifásica
Em das tabelas de água saturada
Substituindo os valores na equação
Passo 6
A massa é dada por
O estado final é vapor saturado, sabemos que o volume é
Sabendo os volumes nos dois estados, e que a pressão é constante em um sistema pistão-cilindro, resolvendo para o trabalho
Passo 7
A energia interna no estado 1 é dada por
Para das tabelas de água saturada
Substituindo os valores para o tempo