Um sistema que consiste em 1 kg de H2O é submetido a um ciclo de potência composto pelos seguintes processos:
Processo 1-2: aquecimento isocórico desde p1 = 5 bar e T1 = 160°C até p2 = 10 bar.
Processo 2-3: resfriamento isobárico até o estado de vapor saturado.
Processo 3-4: resfriamento isocórico até T4 = 160°C.
Processo 4-1: expansão isotérmica com Q41 = -815,8 kJ.
Esboce o ciclo em diagramas p–υ e T–υ. Desprezando os efeitos das energias cinética e potencial, determine a eficiência térmica.
Passo 1
Ooopa, beleza?
Vamos lá pra mais uma questão bem interessante de termodinâmica!
Passo 2
É dado que:
- Processo 1-2: Aquecimento a pressão constante a de um vapor saturado
- Processo 2-3: Resfriamento a volume constante a e
- Processo 3-4: Compressão isotérmica com
- Processo 4-1: Aquecimento a volume constante
Passo 3
Diagrama e
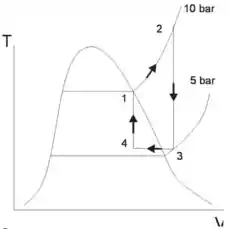
Passo 4
Agora vamos achar o trabalho durante o processo 1-2:
No estado 1 o volume específico é obtido da tabela de vapor de água superaquecido
Passo 5
O calor transferido durante o processo 1-2. Da tabela de pressão para as propriedades de saturação da água quando temos o valor de .
Já que está entre e na tabela de propriedades de água superaquecida, é obtida interpolando
O balanço de energia é expresso como
Passo 6
O calor transferido durante o processo 2-3. Já que é um processo com volume constante, a gente já sabe que
Das propriedades de vapor de água saturada, é obtida interpolando
A transferência de calor é
Passo 7
Vamos achar o trabalho feito no processo 3-4. A gente já sabe a transferência de calor .
Das propriedades de água saturada tabela de pressão, interpolamos entre e
A energia interna é
O trabalho feito durante o processo 3-4 é
Passo 8
A transferência de calor durante o processo 4-1. A gente sabe que o processo é com volume constante, então
O trabalho total então é
Passo 9
A eficiência térmica do ciclo é definida como
A transferência de calor que entra no sistema é definida como positiva são e
Então a eficiência é dada por
Passo 10
Já que é um processo cíclico, podemos notar que a relação abaixo é satisfeita