A água é o fluido de trabalho em um ciclo de Rankine. O vapor superaquecido entra na turbina a 10 MPa e 480°C, e a pressão no condensador é de 6 kPa. A turbina e a bomba têm eficiências isentrópicas de 80 e 70%, respectivamente. Determine para o ciclo:
(a) a taxa de transferência de calor para o fluido de trabalho que passa pelo gerador de vapor, em kJ por kg de vapor que flui.
(b) a eficiência térmica.
(c) a taxa de transferência de calor do fluido de trabalho que passa pelo condensador para a água de resfriamento, em kJ por kg de vapor que flui.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
O diagrama do ciclo Rankine
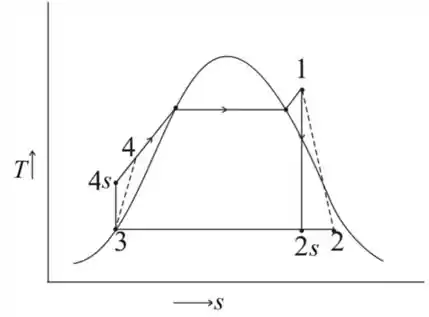
Passo 3
Obtendo as propriedades do vapor a pressão e temperatura das tabelas de vapor superaquecido
Obtendo as propriedades de água no condensador a pressão da tabela de vapor saturado
Passo 4
O processo 1-2s é uma expansão isentrópica, então
Achando a entalpia no estado 2s
Achando a entalpia atual no estado 2 usando a eficiência isentrópica da turbina
Passo 5
A entalpia e o volume específico no estado 3 é igual ao líquido saturado no condensador a pressão
Achando o trabalho da bomba usando a bomba isentrópica no processo 3-4s
Passo 6
Achando o trabalho atual na bomba usando a eficiência isentrópica da bomba
Aplicando a primeira lei ao processo 3-4 e achando a entalpia no estado 4
Passo 7
a) Achando a transferência de calor para o fluido passando pelo gerador de vapor
Passo 8
c) Achando a transferência de calor para o condensador
Passo 9
b) Achando a eficiência térmica
Resposta
a)
b)
c)