A água é o fluido de trabalho em um ciclo ideal de Rankine. O vapor entra na turbina a 1400 lbf/in2 e 1000°F. A pressão no condensador é de 2 lbf/in2. A potência líquida de saída do ciclo é 1 × 109 Btu/h. A água de resfriamento sofre um acréscimo de temperatura de 60°F a 76°F, com queda de pressão desprezível, ao passar pelo condensador. Determine para esse ciclo:
(a) a vazão mássica de vapor, em lb/h.
(b) a taxa de transferência de calor, em Btu/h, para o fluido de trabalho que passa pelo gerador de vapor.
(c) a eficiência térmica.
(d) a vazão mássica da água de resfriamento, em lb/h.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
Desenhando o diagrama do ciclo de Rankine
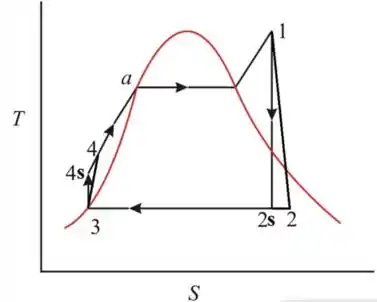
Passo 3
Estado 1
Obtendo as propriedades da água a pressão de e temperatura de da Tabela A-4E “Propriedades de Vapor de Água Superaquecida”
Estado 2
Obtendo as propriedades da água no condensador a pressão de da Tabela A-3E “Propriedades de Água Saturada: Tabela de Pressão”
Obtendo a entalpia da água a água resfriando a temperatura de da Tabela A-2E “Propriedades de Água Saturada: Tabela de Temperatura”
Obtendo a entalpia da água a água resfriando a temperatura de da Tabela A-2E “Propriedades de Água Saturada: Tabela de Temperatura”
Passo 4
Considerando o processo 1-2s uma expansão isentrópica na turbina
Achando a entalpia no estado 2s
Achando a entalpia atual no estado 2 usando a eficiência isentrópica da turbina
Achando a entalpia no estado 3
Achando o volume específico no estado 3
Passo 5
O processo 3-4s é um trabalho de bomba isentrópica. Aplicando a equação da energia
Achando a entalpia atual no estado 4 usando a eficiência isentrópica para a bomba
Passo 6
a) achando a taxa de vazão mássica do vapor
Passo 7
b) achando a taxa de calor transferido para o fluido passando pelo gerador
Passo 8
c) Achando a eficiência térmica do ciclo
Passo 9
d) Aplicando o balanço de massa no condensador para achar a mtaxa de vazão mássica no condensador
Resposta
a)
b)
c)
d)