Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 2.Problemas - Ex. 75
A água a montante de Hoover Dam, em Nevada, está acima do Rio Colorado. A que taxa deve passar a água pelas turbinas hidráulicas dessa barragem para produzir de potência considerando as turbinas são eficientes?
Passo 1
O exercício pede que a gente determine a vazão mássica de água que tem que passar por uma turbina eficiente para gerar de potência. Como essa turbina possui eficiência máxima, ela converte toda a energia potencial da água que está mais alta em potência! Todos os dados fornecidos pelo enunciado estão presentes na figura abaixo.
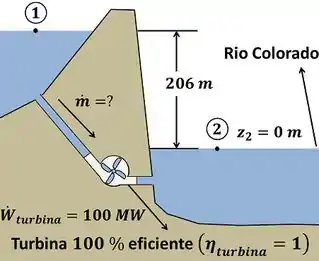
Para calcular , temos que calcular primeiro a taxa de variação energia potencial da água através da fórmula da eficiência da turbina .
onde é a potência gerada pela turbina que vale . vale segundo o enunciado.
O próximo passo é calcular a variação de energia potencial da água através da variação de energia potencial.
Passo 2
onde é a aceleração da gravidade da Terra que vale , é a variação de altura da água do reservatório mais baixo pro reservatório mais alto e é a vazão mássica de água.
O valor de é mostrado na figura. Quando a água se desloca do ponto para o ponto , ela diminui sua altitude em .
Se a gente igualar essa fórmula de com a fórmula da variação de energia potencial da água em função da eficiência da turbina, conseguimos criar uma equação para .
Mas cuidado! Para calcular corretamente, precisamos converter de para
Fazemos isso usando a fórmula abaixo.
Agora que temos todos os valores que precisamos, vamos calcular .
Passo 3
Antes de calcular , vamos converter a unidade de .
Com esse valor, encontramos