Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 5.Problemas - Ex. 2

Analise um ciclo de Carnot para o caso especial de um corpo paramagnético ideal, a fim de mostrar que a razão entre duas temperaturas empíricas, definidas pela lei de Curie, θ 1 = C c h M , é igual à razão entre as temperaturas termodinâmicas correspondente. A energia interna de um corpo paramagnético ideal depende somente de T , e durante um processo adiabático h θ 1 permanece constante.

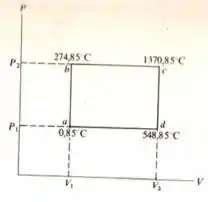
Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de termodinâmica de Sears e Salinger por meio da análise um ciclo de Carnot para o caso especial de um corpo paramagnético ideal, a fim de mostrar que a razão entre duas temperaturas empíricas, definidas pela lei de Curie, θ 1 = C c h M , é igual à razão entre as temperaturas termodinâmicas correspondente. A energia interna de um corpo paramagnético ideal depende somente de T , e durante um processo adiabático h θ 1 permanece constante.

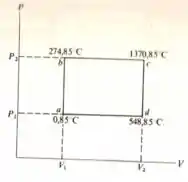
Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Passo 2

Então galerinha analisando as temperaturas nos pontos definidos por

P a = 0,85 ° C ,     P b = 274,85 ° C ,     P c = 1370,85 °     e     P d = 548,85 ° C

Utilizando da equação de Curie:

θ 1 = C c h M

Ficando,

θ a b = 274,85 0,85             θ c d = 1370,85 548,85

Chegando em,

θ a b = 323,35 ° C             θ c d = 2,49 ° C

Ficando a sua definição geral representada pela soma que vale

325,35 + 2,49 = 325,84

Com isso,

T t = 325,84 ° C

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

T t = 325,84 ° C

Exercícios de Livros Relacionados

O ciclo padrão de ar de Carnot não foi mostrado no texto; mostre o diagrama T - s para esse ciclo. Em um ciclo padrão de ar de Carnot, a temperatura baixa é de 280K e o rendimento é de 60 % . Se a pre
Em um conjunto cilindro-pistão, ar é submetido a um ciclo de Carnot, onde T L = 26,8° C e o rendimento total do ciclo é η = 2 / 3 . Determine T H , o trabalho específico e a razão de volume na expansã
O refrigerante R-22 é usado como fluido de trabalho em um ciclo de bomba de calor convencional. Vapor saturado entra no compressor dessa unidade a 10° C ; a temperatura do vapor medida na saída do com
Considere uma bomba de calor ideal, com temperatura no condensador de 50° C e temperatura no evaporador de 0° C . Determine o coeficiente de performance desse aparelho para os fluidos de trabalho R-12
O desempenho de um refrigerador, trabalhando num ciclo por absorção de amônia, deve ser comparado com o de um sistema de refrigeração por compressão de vapor. Considere um sistema de absorção com uma