Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 83

Argônio está contido em um cilindro equipado com um pistão. Inicialmente, o argônio está a 100 kPa e 27 °C, ocupando um volume de 0,4 m³. O argônio é então comprimido enquanto a temperatura é mantida constante, até que seu volume seja de 0,2 m³. Em seguida, o argônio expande-se, enquanto a pressão é mantida constante até que o volume seja de 0,6 m³.

  1. Esboce ambos os processos em um único diagrama P-V mostrando a direção dos processos e identifique os estados finais como 1, 2 e 3.
  2. Determine a quantidade total de calor líquido transferido para o argônio, em kJ, durante os processos combinados.

Passo 1

O diagrama P-V que representa os processos presentes no sistema é mostrado na figura abaixo:

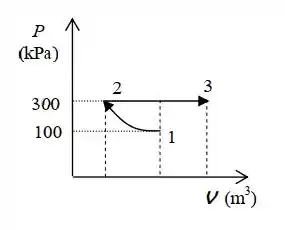
Passo 2

O processo 1-2 é isotérmico, enquanto que o processo 2-3 é isobárico. Para o argônio R = 0,2801 kJ/kg ⋅ K e c v = 0,3122 kJ/kg ⋅ K (Tabela A-2a). Dessa forma, a massa de ar contida no cilindro é

m = P 1 V 1 R T 1 = 100 ⋅ 0,4 0,2081 ⋅ 300 = 0,6407   k g

Em 2, a pressão é:

P 2 = P 1 V 1 V 2 = 100 ⋅ 0,4 0,2 = 200   k P a

Em 3, temperatura é:

T 3 = T 2 V 3 V 2 = 300 ⋅ 0,6 0,2 = 200   k P a

Passo 3

O balanço de energia no sistema para o processo 1-3 pode ser expresso por:

W i n , 1 - 2 + Q i n - W o u t , 2 - 3 = Δ U = m c v ( T 3 - T 1 )

Os trabalhos de compressão e expansão são dados por:

W i n , 1 - 2 = m R T 1 ln ⁡ V 2 V 1 = 0,6407 ⋅ 0,2081 ⋅ 300 ⋅ ln ⁡ 0,2 0,4 =   - 27,7   k J → W i n , 1 - 2 = 27,7   k J

W o u t , 2 - 3 = P 2 V 3 - V 2 = m R T 3 - T 2 = 0,6407 ⋅ 0,2081 ⋅ 900 - 300 = 80,0   k J

Substituindo esses valores na equação de balanço de energia:

Q i n = W o u t , 2 - 3 - W i n , 1 - 2 + m c v T 3 - T 1 = 80 - 27,7 + 0,6407 ⋅ 0,3122 ⋅ 900 - 300 = 172,2   k J

Resposta

Q i n = 172,2   k J

Ver Outros Exercícios desse livro