Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 36

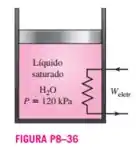
Um arranjo pistão-cilindro isolado contém 0,8 L de água líquida saturada a uma pressão constante de 120 kPa. Um aquecedor a resistência elétrica dentro do cilindro é ligado, e um trabalho elétrico de 1.400 kJ é realizado na água. Considerando que a vizinhança está a 25 °C e 100 kPa, determine (a) o trabalho mínimo com o qual esse processo pode ser realizado e (b) a exergia destruída durante esse processo.

Passo 1

Vamos começar determinando as propriedades da água líquida saturada

P 1 = 120   k P a

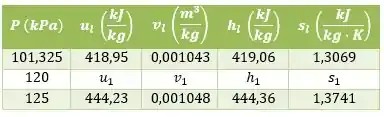
Infelizmente, a Tabela A5 não tem os valores para essa pressão, termos que interpolar

u 1 = 444,23 - 417,40 125 - 100 120 - 100 + 417,40 = 439,18 k J k g

v 1 = 0,001048 - 0,001043 125 - 100 120 - 100 + 0,001043 = 0,001047 m 3 k g

h 1 = 444,36 - 419,06 125 - 100 120 - 100 + 419,06 = 439,3 k J k g

s 1 = 1,3741 - 1,3069 125 - 100 120 - 100 + 1,3069 = 1,3607 k J k g   K

Passo 2

Podemos calcular a massa do sistema:

m = V v 1 = 0,008   m 3 0,001047   m 3 / k g = 7,639   k g

Passo 3

O trabalho elétrico é absorvido pela água, de forma que:

W e = m h 2 - h 1

h 2 = W e m + h 1

h 2 = 1400   k J 7,639   k g + 439,3 k J k g

h 2 = 622,57 k J k g

Passo 4

A pressão ao longo de todo o processo é constante, com a entalpia calculada no passo anterior podemos determinar as demais propriedades. Vamos ter que fazer algumas interpolações novamente.

Vamos aproveitar alguns valores do Passo 1

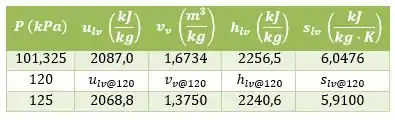
P 2 = 120   k P a ⇒ T a b e l a   A 5   u l = u 1 = 439,18 k J k g v l = v 1 = 0,001047 m 3 k g h l = h 1 = 439,30 k J k g s l = s 1 = 1,3607 k J k g   K

Vamos pegar outros valores importantes na tabela:

u l v @ 120 = 2068,8 - 2087 125 - 101,325 120 - 101,325 + 2087 = 2072,4 k J k g

v v @ 120 = 1,3750 - 1,6734 125 - 101,325 120 - 101,325 + 1,6734 = 1,4285 m 3 k g

h l v @ 120 = 2240,6 - 2256,5 125 - 101,325 120 - 101,325 + 2256,5 = 2243,7 k J k g

s l v @ 120 = 5,91 - 6,0476 125 - 101,325 120 - 101,325 + 6,0476 = 5,93687 k J k g   K

Passo 5

Agora que temos as propriedades à 120 kPa, podemos calcular as propriedades da mistura.

Primeiro calculamos a titulação:

x 2 = h 2 - h l h l v = 622,57 - 439,30 2243,7 = 0,08168

Utilizando o título podemos calculas as demais propriedades:

s 2 = s l + x 2 ⋅ s l v = 1,3607 + 0,08168 ⋅ 5,93687 = 1,8456 k J k g   K

u 2 = u l + x 2 ⋅ u l v = 439,18 + 0,08168 ⋅ 2072,4 = 608,45 k J k g

v 2 = v l + x 2 v v - v l = 0,001047 - 0,08168 1,4285 - 0,001047 = 0,1176 m 3 k g

Passo 6

Item A)

Vamos aplicar o balanço de exergias:

X e n t - X s a i - X d e s t = Δ X

Para um sistema reversível a destruição de exergia deve ser igual a zero. Aplicando no nosso sistema, a variação de exergia representa o trabalho:

W r e v = X 2 - X 1

Aplicando a Equação 8-16

W r e v = m u 2 - u 1 + P 0 v 2 - v 1 - T 0 s 2 - s 1

W r e v = 7,639 ⋅ 608,45 - 439,18 + 100 0,1176 - 0,001047 - 298 1,8456 - 1,3607

O trabalho reversível

W r e v = 278,25   k J

Passo 7

Item B)

Vamos aplicar um balanço de entropia no sistema:

S e n t - S o u t + S g e n = Δ S

Neste sistema não há entrada nem saída de entropia do sistema, então:

S g e n = Δ S

S g e n = m s 2 - s 1

S g e n = 7,639 1,8456 - 1,3607

S g e n = 3,704 k J k g

Passo 8

A exergia destruída pode ser calculada por sua definição:

X d e s t r = T 0 S g e n

X d e s t r = 298 ⋅ 3,704

X d e s t r = 1103,8   k J

Resposta

  1. W r e v = 278,25   k J
  2. X d e s t r = 1103,8   k J
Ver Outros Exercícios desse livro