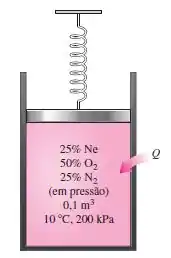
Um arranjo pistão-cilindro com mola contém uma mistura de gases cujas frações de pressão correspondem a , e . O diâmetro do pistão e a mola são selecionados para esse dispositivo e devem atender às seguintes exigências: o volume deve ser de , quando a pressão for de , quando a pressão for de . Inicialmente, o gás é fornecido ao dispositivo até que a pressão seja de, e a temperatura, . O dispositivo é então aquecido até que a pressão seja de . Calcule o trabalho total e a transferência de calor para esse processo.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Para uma mistura de gases ideais, a fração molar, a fração em volume e a fração em pressão de um componente são idênticas. Portanto, a partir do volume, podemos dizer que:
A fração molar de nitrogênio, será:
A fração molar de Oxigênio, corresponde a:
E a fração molar de será:
Passo 2
As pressões parciais dos gases são dadas pelo produto entre a fração molar e a pressão total da mistura. Logo:
A pressão parcial do Oxigênio será:
E a pressão parcial de Neônio será:
Passo 3
A massa molar da mistura pode ser expressa como:
Portanto, temos que a massa molar da mistura será:
De acordo com a tabela de propriedades, temos que:
Logo:
Passo 4
A constante de gás aparente da mistura pode ser dada por:
Passo 5
As frações de massa dos gases também podem ser calculadas:
Aplicando aos nossos gases, temos que:
Para o Nitrogênio, temos que:
E para o argônio, temos que:
Passo 6
O calor especifico a volume constante da mistura é dado por:
Precisamos saber os calores específicos de cada gás. Estes valores também estão disponíveis nas tabelas:
Portanto:
Passo 7
A massa do sistema será:
Por interpolação podemos descobrir o volume após a transferência de calor:
A temperatura final será:
O trabalho durante o processo será:
O calor fornecido é dado por: