Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 14.Problemas - Ex. 81
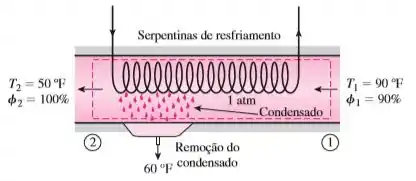
Ar atmosférico úmido a 1 atm, 90 °F e 90% de umidade relativa é resfriado até 50 °F, enquanto a pressão de mistura permanece constante. Calcule a quantidade de água (em lbm/lbm de ar seco) retirada do ar e a necessidade de resfriamento (em Btu/ lbm de ar seco), considerando que a água no estado líquido deixa o sistema a 60 °F.
Passo 1
Este é um processo de fluxo constante e, portanto, a vazão mássica do ar seco permanece constante durante todo o processo (.
Ar seco e vapor de água são gases ideais.
As mudanças de energia cinética e potencial são insignificantes.
Os estados de entrada e saída do ar são completamente especificados e a pressão total é de 1 atm. As propriedades do ar em vários estados são determinadas a partir da tabela psicrométrica (Figura A-31E) como:
E
E também,
Passo 2
A quantidade de umidade no ar diminui devido à desumidificação (. Aplicando as equações do balanço de massa de água e balanço de energia na seção combinada de resfriamento e desumidificação:
Balanço de Massa de Água:
Equilíbrio energético: