Um avião a jato está voando a uma altitude de , onde a pressão ambiente é de aproximadamente e a temperatura ambiente é de . A velocidade do avião é de , a razão de pressão através do compressor é 14:1 e a temperatura máxima do ciclo é de . Considere que o escoamento de entrada passa através de um difusor até uma velocidade relativa zero no estado 1. Determine a temperatura e a pressão no estado 1 e a velocidade (relativa ao avião) do ar saindo do motor a .
Passo 1
Fala, galera! Vamos resolver essa questão.
Vamos começar dando uma olhada no diagrama do ciclo:
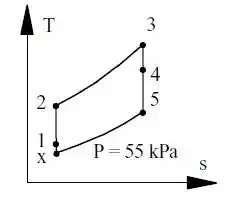
Temos as condições ambiente:
E velocidade:
Vamos supor que o ar nesse estado seja reversivelmente desacelerado até a velocidade zero e, em seguida, ele entra no compresso em 1.
Temos ainda as condições:
Passo 2
Beleza, galera. Vamos determinar a temperatura no estado 1 através da equação:
E para a pressão, temos a relação isentrópica:
Passo 3
Vamos analisar agora o volume de controle do compressor. Utilizando a relação isentrópica:
Pela equação de energia, temos:
Pela relação de compressão:
Calculando a pressão na turbina, temos:
E para o bocal:
E a velocidade do ar saindo do motor é dada por:
Portanto, a velocidade é:
E concluímos o exercício. Valeu, galera! 😉