Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 143
Um avião a turbojato está voando a uma velocidade de 320 m/s e a uma altitude de 9.150 m, a 32 kPa e 32 °C. A razão de pressão no compressor é de 12, e a temperatura na entrada da turbina é de 1.400 K. Ar entra no compressor a uma vazão de 60 kg/s, e o combustível do jato tem um poder calorífico de 42.700 kJ/kg. Considerando um funcionamento ideal de todos os componentes e calores específicos constantes do ar à temperatura ambiente, determine
- a velocidade dos gases de exaustão
- a potência de propulsão desenvolvida
- a taxa de consumo de combustível.
Passo 1
Vamos assumir que:
Existem condições operacionais estáveis.
As premissas do padrão aéreo são aplicáveis.
O ar é um gás ideal com aquecimentos específicos constantes à temperatura ambiente.
As energias cinética e potencial são desprezíveis, exceto na entrada do difusor e na saída do bico.
A saída de trabalho da turbina é igual à entrada de trabalho do compressor.
Sabemos que as propriedades do ar à temperatura ambiente são e
Assumimos que a aeronave está estacionária e o ar está se movendo em direção à aeronave a uma velocidade de . Idealmente, o ar deixará o difusor com uma velocidade desprezível .
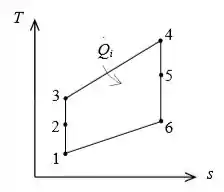
Vamos observar a figura:
Passo 2
Agora vamos achar os valores:
No difusor:
No compressor:
Na turbina:
No bocal, achando a velocidade procurada:
Passo 3
Na letra b teremos a potência de propulsão desenvolvida
Passo 4
Na letra c teremos a taxa de consumo de combustível.