Com base na Eq. 11.122,
(a) calcule ln f para um gás que obedece à equação de estado de Redlich-Kwong.
(b) Utilizando o resultado do item (a), calcule a fugacidade, em bar, para o Refrigerante 134a a 90°C e 10 bar. Compare o resultado com o valor da fugacidade obtido a partir do diagrama generalizado de fugacidade.
Passo 1
E aiiii , vocês estão prontos crianças??
Estamos capitão rs, parei galeraaa, bora lá?
- Vamos escrever a equação da fugacidade
- Da tabela de propriedades críticas de substâncias selecionadas, para o refrigerante R134a
Para integrar o lado direito da equação (1), considere o diagrama de um gás que obedece á equação de Redlich-Kwong :
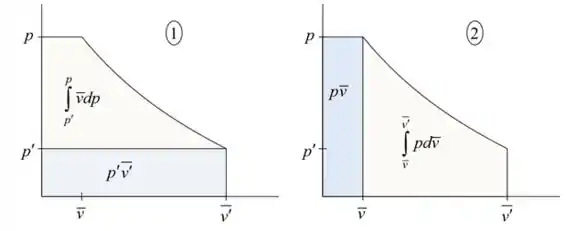
Passo 2
Interprete a área do gráfico de duas maneiras, conforme mostrado na figura anterior. Como as duas áreas são iguais, temos:
Substituindo a equação (2) na equação (1), temos:
Vamos escrever a equação de Redlich-Kwong
Passo 3
Agora vamos substituir a equação de Redlich-Kwong na expressão (3)
Avaliando as integrais
Passo 4
Agora iremos considerar os limites como na temperatura fixa T
Logo,
Sendo assim a equação (4),fica da seguinte maneira
Substitua o fator de compressibilidade Z por
Passo 5
Vamos considerar a equação de Redlich-Kwong
Multiplique por em ambos os lados e substitua Z por ,
Substitua a equação (6) na equação (5)
Portanto, a equação (7) é a relação necessária.
Passo 6
Temperatura crítica
Pressão crítica,
Temperatura do refrigerante
.
.
Pressão do refrigerante
Temperatura reduzida
Pressão reduzida
Passo 2
Partindo do gráfico do coeficiente de fugacidade generalizado, no
O coeficiente de fugacidade é
Sendo assim, a fugacidade do gás de acordo com o gráfico é de 9.2 bar
Calcularemos os coeficientes de van der Waal para o refrigerante R134a
Onde
Onde
Passo 3
Vamos substituir os valores obtidos dos coeficientes de van der Waal junto com os valores da constante universal do gás, pressão e temperatura de Redlich-Kwong para obter
Resolvendo a equação quadrática acima, iremos obter:
Substituindo os valroes obtidos na equação (7), para podermos obter a fugacidade, temos:
A fugacidade do refrigerante calculada é 9.1 bar
Pode se observar que os valores obtidos do gráfico e dos cálculos quase concordam entre si.
Resposta
Vide o passo a passo!