Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 2.Problemas - Ex. 76
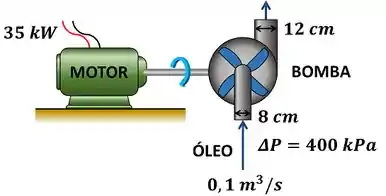
Uma bomba de óleo consome de potência elétrica para bombear óleo com a uma vazão de . Os diâmetros dos tubos de entrada e saída são de e de , respectivamente. Considerando que o aumento da pressão do óleo na bomba e de e a eficiência do motor corresponde a , determine a eficiência mecânica da bomba.
Passo 1
O enunciado fala sobre duas de transformações de energia. A primeira transformação é feita pelo motor. Ele transforma de energia elétrica que ela recebe em potência de giro do eixo com uma eficiência de . A segunda transformação é feita pela bomba. Ela recebe a potência de giro do eixo e transforma em energia mecânica do óleo . O exercício quer saber a eficiência da segunda transformação feita pela bomba .
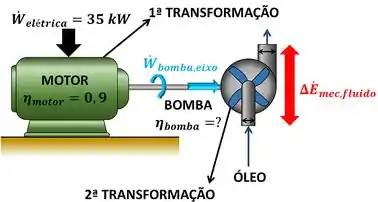
A fórmula de eficiência da bomba é mostrada abaixo:
é a potência de giro do eixo. Ela é o resultado da primeira transformação de energia. Por isso, ela é igual à potência elétrica que o motor recebeu multiplicada pela eficiência dessa transformação de energia .
Só falta aprender a calcular a variação de energia mecânica do óleo para calcular a eficiência da bomba . Vamos fazer isso no próximo passo!
Passo 2
A bomba varia a energia mecânica do óleo de duas formas: diminuindo sua energia cinética e aumentando sua energia através da pressão. Ou seja, é a soma desses dois fatores.
Nessa equação, é a vazão mássica do óleo. é a velocidade do óleo depois de ser bombeado. é a velocidade do óleo antes de ser bombeado. é a variação de pressão do óleo através da bomba. E é densidade do óleo. O enunciado fala diretamente o valor de e .
Atenção! foi dado em quilopascal ! Precisamos converter para pascal para a variação de energia relacionada à pressão ficar em watt igual a variação de energia cinética!
A questão informa o valor das variáveis , e indiretamente. As três são calculadas através da vazão volumétrica de óleo que é dada pelo enunciado.
é a área da tubulação de sucção da bomba. O diâmetro dessa tubulação vale . é a área da tubulação de descarga da bomba. O diâmetro dessa tubulação vale .
Agora que temos todas as informações que precisamos, vamos calcular no passo seguinte.
Passo 3
A potência de giro do eixo vale:
Para calcular precisamos calcular primeiro .
Em segundo lugar, precisamos calcular as velocidades do óleo.
Por fim, podemos calcular .
Atenção! Como o está em quilowatt , precisamos converter para também!
Agora podemos achar o valor da eficiência bomba.