Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 2.Problemas - Ex. 77
Uma bomba cuja eficiência é de e a potência de entrada corresponde a está bombeando água a partir de um lago para um reservatório próximo a uma taxa de por um tubo de diâmetro constante. A superfície livre do reservatório está a acima do lago. Determine a potência mecânica utilizada para superar os efeitos de atrito na tubulação.
Passo 1
A questão fala sobre uma bomba que recebe de potência e converte essa potência em dois tipos de taxa de energia com uma eficiência de . Um dos tipos é a taxa de energia que a água precisa para vencer o atrito das tubulações e o outro tipo é a taxa de energia que a água precisa para variar sua energia potencial gravitacional . O exercício que saber justamente quanto vale .
Para calcular esse valor, vamos precisar dos dados mostrados pela figura abaixo.
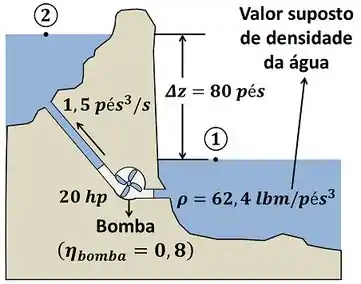
O taxa de energia necessária pra vencer o atrito é igual à taxa de energia que a bomba recebe e converte em energia útil para água menos a taxa de energia que a água precisa receber para variar sua energia potencial gravitacional .
Mas é a taxa de energia que a bomba recebe multiplicada pela eficiência da bomba .
será calculado no passo a seguir.
Passo 2
A variação de energia potencial gravitacional pode ser calculada com a fórmula abaixo.
onde é a aceleração da gravidade da Terra que vale , é a variação de altura da água do lago pro reservatório mais alto e é a vazão mássica de água.
O valor de é mostrado na figura. Quando a água se desloca do ponto para o ponto , ela se eleva em .
Já precisa ser calculado a partir da vazão volumétrica da água dada pelo enunciado. Convertemos em , multiplicando pela densidade da água .
A vazão volumétrica da água é dada pela questão.
Atenção! O exercício não fala quanto vale o da água líquida a temperatura ambiente. Mas podemos considerar que ele vale em unidades inglesas!
Com essas unidades, o valor de será encontrado em . Para converter esse valor para , temos que dividí-lo por .
Pronto! Já temos todas as informações necessárias para calcular . Então vamos iniciar as contas no próximo passo.
Passo 3
Iniciamos o cálculo de a partir da vazão mássica de água que passa pela bomba.
Com esse valor, podemos achar .
Convertendo para , o valor vira:
Só falta calcular para calcular .
Substituindo na fórmula de :