Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 152
Calcule a destruição de energia associada a cada um dos processos do ciclo Brayton descrito no Prob. 9–89, considerando que a temperatura da fonte é de 1.600 K e que a temperatura do sumidouro é igual a 310 K
Passo 1
Vamos lá! Para começar com o pé direito, vamos dar uma olhadinha no comportamento do ciclo Brayton:
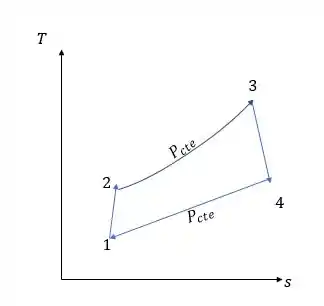
Queremos calcular a destruição de energia associada em cada um dos processos do ciclo Brayton, ou seja, a gente quer em , , e .
O problema não nos da as informações de entropia nos pontos, mas nos da outras informações, com elas a gente pode ir até a tabela no fim do livro e pegar as entropias padrão para cada ponto:
Outras informações importantes que a gente pode tirar do problema :
E a razão das pressões:
Passo 2
Vamos começar pelo processo :
Relembrando os dados:
Substituindo:
Passo 3
Para o processo , temos:
Entre os pontos e a pressão é constante, logo:
Os dados são:
Substituindo:
Passo 4
Para o processso :
O problema nos da a razão das pressões:
Observando as curvas com pressão constante temos:
Logo:
As entropias padrão são:
Substituindo:
Calculando:
Passo 5
gora vamos calcular o processo :
Sabemos que a pressão , logo:
Temos os dados:
Substituindo:
Calculando:
Uhuuuuul!!!