Uma casa com aquecimento solar passivo, perdendo calor para o exterior a uma taxa média de 50000 kJ/h, é mantida por 10 horas durante uma noite de inverno. A casa deve ser aquecida por 50 reservatórios de vidro, cada um contendo 20 L de água, que é aquecida a 80 °C durante o dia pela absorção de energia solar. Um aquecedor elétrico reserva de 15 kW, controlado por termostato, é ligado sempre que necessário para manter a casa a 22 °C. (a) Por quanto tempo o sistema de aquecimento elétrico funcionou nessa noite? (b) Por quanto tempo o aquecedor elétrico precisaria funcionar nessa noite se a casa não tivesse nenhum aquecimento solar?
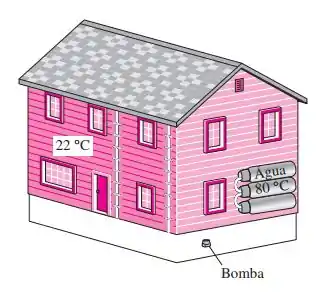
Passo 1
A água é considerada como substância incompressível com calor específico constante. A massa de água, com = 1 kg/L, é:
A equação de balanço de energia para o sistema é:
Substituindo os valores na equação acima:
Passo 2
Se a casa não tivesse aquecimento solar, a equação de balanço de energia fica:
Substituindo os valores na equação acima: