Enunciado
Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 14.Problemas - Ex. 77
Um ciclo de potência simples com base em uma turbina a gás operando em regime permanente, com ar como substância de trabalho, é mostrado na Fig. P14.64. Dentre os componentes do ciclo está um compressor de ar montado no mesmo eixo da turbina. O ar é aquecido no trocador de calor a alta pressão antes de entrar na turbina. O ar que sai da turbina é resfriado no trocador de calor a baixa pressão antes de retornar ao compressor. Os efeitos das energias cinética e potencial são desprezíveis. O compressor e a turbina operam adiabaticamente. Usando o modelo de gás ideal para ar, determine a (a) potência requerida pelo compressor, em hp, (b) a potência de saída da turbina, em hp, e (c) a eficiência térmica do ciclo.
Passo 1
Faaaaaala galera, bora pra mais um??
Então so vamo!
Primeiro vamos desenhar o diagrama esquemático do ciclo de potência simples da turbina a gás.
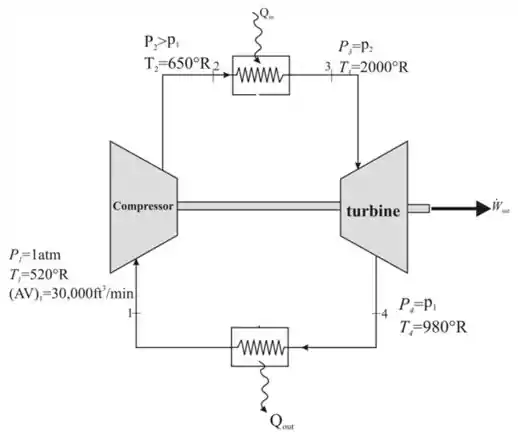
Passo 2
Pela tabela A-22E
Em 520°R
Entalpia no estado 1
Em 650°R (USANDO INTERPOLAÇÃO)
Entalpia no estado 2
Em 2000°R
Entalpia no estado 3
Em 980°R
Entalpia no estado 4
Passo 3
Determinaremos a taxa de fluxo de massa de ar
Passo 4
- Vamos calcular a potência necessária para o compressor.
- Calcularemos agora a potência de saída da turbina
- Iremos calcular a eficiência térmica do ciclo
Iremos substituir os valores conhecidos
Portanto, a potencia necessária para o compressor é 1686.56 hp
Passo 5
Substituindo os valores
Portanto a potência de saída da turbina é .
Passo 5
Substituindo
Portanto, a eficiência térmica do clico é de 67.99%
Resposta
- Portanto, a potencia necessária para o compressor é 1686.56 hp.
- Portanto a potência de saída da turbina é .
- Portanto, a eficiência térmica do clico é de 67.99%