Enunciado
Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 8.Problemas - Ex. 6
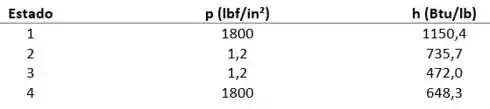
Um ciclo de potência a vapor de Carnot opera com água como fluido de trabalho. O líquido saturado entra na caldeira a 1800 lbf/in² e o vapor saturado entra na turbina (estágio 1). A pressão no condensador é de 1,2 lbf/in². A vazão mássica de vapor é 1 x lb/h. Os dados nos pontos característicos do ciclo são fornecidos na tabela a seguir. Determine
(a) a eficiência térmica.
(b) a relação entre o trabalho de entrada na bomba e o trabalho desenvolvido pela turbina – bwr.
(c) a potência líquida desenvolvida, em Btu/h.
(d) a taxa de transferência de calor para o fluido de trabalho que passa pela caldeira.
Passo 1
Faaaaaaala galera!!! Vamos começar expondo as hipóteses trabalhadas?
1 – Cada componente do ciclo vai ser analisado como um volume de controle em regime estacionário, com uma entrada e uma saída de fluido.
2 – Todos os processos sobre o fluido de trabalho apresentam reversibilidades internas.
3 – A turbina e a bomba operam adiabaticamente.
4 – Os efeitos das energias cinética e potencial são desprezíveis.
Vamos agora dar uma organizada nos dados:
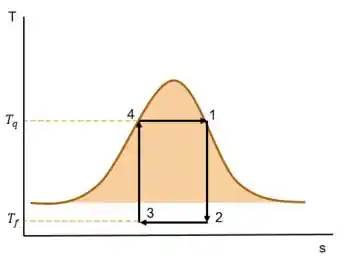
E com isso já podemos definir as propriedade de cada um dos estados no ciclo! Antes vamos dar uma desenha no gráfico T-s desse ciclo para enxergarmos melhor e em seguida vamos fazer o próximo passo.
Passo 2
Começamos dando uma analisada nas informações da tabela, enunciado e gráfico! Quem são essas temperaturas quente e frias?
A temperatura quente é a temperatura dos estados 1 e 4! Ambos estados estão a uma pressão de 1800 lbf/in² e com o fluido saturado! Então vamos dar uma olhada na tabela A-3E para sabermos qual a temperatura de saturação à essa pressão:
Para a temperatura fria , fazemos o processo análago ao anterior! Vamos na tabela A-3E ver a temperatura de saturação a uma pressão de 1,2 lbf/in²:
Vamos partir para os cálculos pedidos!
Passo 3
Na letra (a) ele nos pede a eficiência térmica! Para o ciclo de Carnot temos:
Substituindo os dados:
Tranquilo né? Vamos seguir em frente
Passo 4
Já na letra (b) é pedido a razão entre o trabalho de entrada da bomba e o trabalho desenvolvido pela turbina! Ou seja, o bwr (Back Work Ratio)!
Lembrando que a turbina fica situada entre o estado 1 e o 2, e a bomba entre o 3 e o 4!!!
Substituindo os valores pelos da tabela:
Moleza né? Faltam só mais duas letras, aguenta fime aí!
Passo 5
Agora na letra (c) é pedido o trabalho do ciclo! É só fazermos:
Substituindo pelos dados, vamos ter:
Bem tranquilo! Vamos agora para o último passo!
Passo 6
Na letra (d) temos que calcular a taxa de transferência de calor que passa pela caldeira, ou seja, no evaporador! O evaporador se encontra entre os estados 4 e 1! Então:
Vamos apenas substituir os dados e acabar a questão!
Finalmente terminamos!!! É isso aí! Já podemos ir para a próxima questão né?
Resposta
(a)
(b)
(c)
(d)