Na costa sul da ilha do Havaí, uma lava flui continuamente para o oceano. Propõe-se a instalação de uma planta de potência flutuante próxima ao fluxo da lava que utilize amônia como fluido de trabalho. A planta se aproveita da variação da temperatura entre a água quente a 130°F próxima à superfície e a água do mar a 50°F a uma profundidade de 500 ft, para produzir energia. A Fig. P8.14 mostra a configuração da planta e fornece alguns outros dados. Utilizando as propriedades da água pura para a água do mar e modelando a planta de potência como um ciclo de Rankine, determine:
(a) a eficiência térmica.
(b) a vazão mássica da amônia em lb/min para uma potência líquida de saída de 300 hp.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
Desenhando o diagrama do ciclo de Rankine
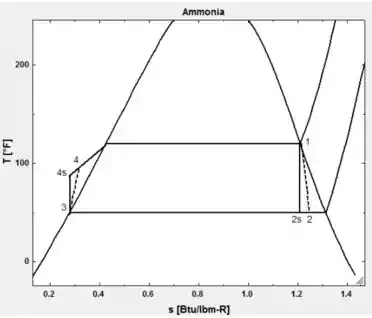
Passo 3
Pegando as propriedades de vapor de amônia saturada a temperatura de da Tabela A-13E “Propriedades de Amônia Saturada (Líquido-Vapor): Tabela de Temperatura”
Pegando as propriedades de vapor de amônia saturada a temperatura de da Tabela A-13E “Propriedades de Amônia Saturada (Líquido-Vapor): Tabela de Temperatura”
O processo 1-2s é um processo isentrópico então, a entropia da amônia no estado 1 e no estado 2s são a mesma
Passo 4
Calculando o título no estado 2s
Calculando a entalpia no estado 2s
Achando a entalpia atual na saída da turbina usando a eficiência isentrópica da turbina
Passo 5
No estado 3, a o fluido é a amônia líquida saturada, pegando as propriedades a temperatura de da Tabela A-13E “Propriedades de Amônia Saturada (Líquido-Vapor): Tabela de Temperatura”
Achando o trabalho isentrópico da bomba
Achando o trabalho atual de entrada usando a eficiência isentrópica da bomba
Achando a entalpia no estado 4 aplicando a primeira lei da termodinâmica ao processo 3-4
Passo 6
a) Calculando a eficiência térmica
Passo 7
b) Calculando a taxa de vazão mássica da amônia usando a potência de saída
Resposta
a)
b)