Enunciado
Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 8.Problemas - Ex. 30
Para o ciclo do problema , reconsidere a análise admitindo que a bomba e cada estágio de turbina tenham uma eficiência isentrópica de
Passo 1
E aí, galerinha! Oia nós aqui de novo!
Bom! É o mesmo exercício do problema anterior! Só mudando uma coisinha! Então, vamo preservar o escopo
E como é de praxe nesse tipo de exercício, a primeira coisa a se fazer, é um esboço do ciclo e do nosso sistema! Isso vai nos ajudar a entender melhor o nosso problema!
Vamos começar fazendo uma representação básica do nosso sistema...
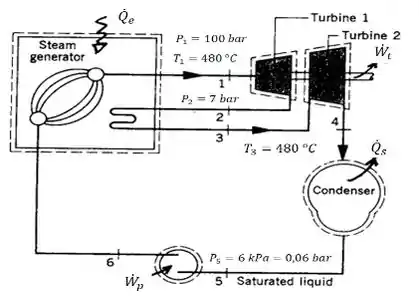
Assim, podemos construir o seguinte gráfico do ciclo de temperatura :
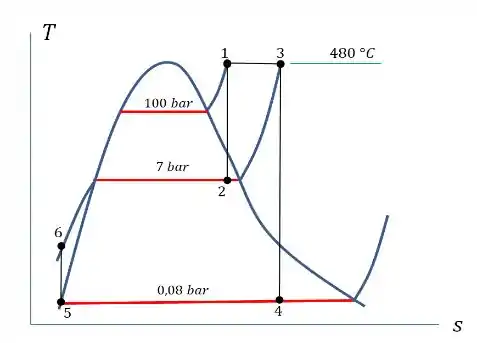
Que beleza de imagem, né não?
Passo 2
Agora, com base em tabelas como a do livro, mostrada abaixo...
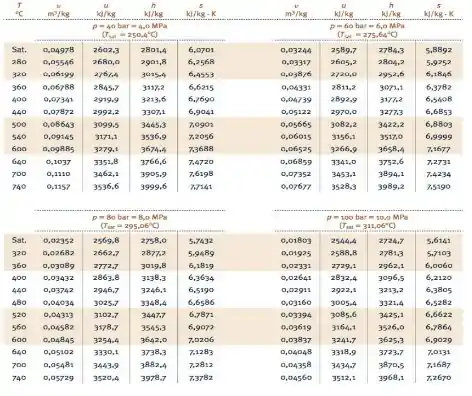
Vamos encontrar as condições referentes aos principais estados destacados na figura do final do !
Para o estado onde , ; temos que:
Para o estado onde , ; temos que:
Logo, com base na tabela abaixo...
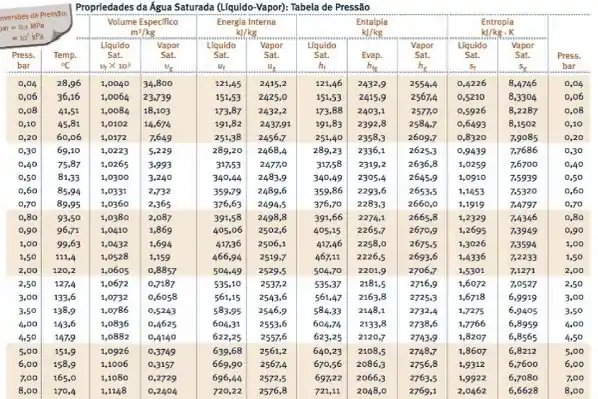
Passo 3
Para o estado , com e :
Para o estado onde , ; temos que:
Logo;
No estado , por sua vez, temos apenas líquido saturado à ...
Passo 4
E finalmente para o estado , falta achar o . Pela figura, podemos ver que...
Pela bibliografia, podemos ver que...
Dessa forma, substituindo os valores numéricos...
Passo 5
a) Que beleza! A parte mais chatinha já foi! Agora, vamos tratar de achar a eficiência!
Analisando o ciclo na figura do , temos que o trabalho do ciclo dividido pela vazão mássica fica assim...
Isso como podemos ver, pode ser reescrito como...
O que nada mais é do que escrever em termos das entalpias que temos!
Assim, substituindo os valores numéricos...
Quanto à quantidade de energia na entrada, que é a nossa taxa de adição de calor, em por de vapor que entra na turbina de primeiro estágio... Ela pode ser escrita como podemos ver na figura do como...
Sendo assim, obtemos que...
b) Que beleza! Pra achar a eficiência então, basta dividir essa segunda pela primeira... Ou seja, a quantidade de entrada pelo trabalho...
c) Por fim, falta achar a taxa de transferência de calor do fluido de trabalho que passa pelo condensador para a água de resfriamento... Que é o nossa quantidade de calor de saída!
Bom! Pelo que podemos ver, ela é dada por...
Pronto! Sucesso, meus queridos!
Resposta
a)
b)
c)