Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 79

Um ciclo Stirling ideal preenchido com ar utiliza um reservatório de energia a 50   ° F como um sumidouro. O motor foi concebido de tal modo que o volume máximo de ar é de 0,5   p é 3 , enquanto o volume mínimo de ar corresponde a 0,06   p é 3 e a pressão mínima é igual a 10   p s i a . O motor deve ser operado de tal forma que deve produzir 2   B t u de trabalho líquido quando 6 Btu de calor forem transferidos externamente para o motor. Determine a temperatura da fonte de energia, a quantidade de ar existente no motor e a pressão máxima de ar durante o ciclo.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Se você não está familiarizado com o ciclo Stirling, observe abaixo o seu diagrama P - v .

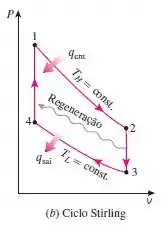
Temos os seguintes dados:

T L = 50 ° F + 460 = 510   ° R

V m á x = 0,5   p é 3

V m í n = 0,06   p é 3

P m í n = 10   p s i a

W l i q = 2   B t u

Q e n t = 6   B t u

Passo 2

A eficiência de um ciclo ideal é dada por:

η = W l i q Q e n t

Da definição, temos também que:

η = W l i q Q e n t = Q e n t - Q s a i Q e n t = 1 - Q s a i Q e n t

Para um ciclo reversível ideal, temos que:

Q e n t Q s a i = T H T L

Logo:

η = 1 - T L T H

Passo 3

Portanto, temos que:

1 - T L T H = W l i q Q e n t

Logo:

1 - 510 T H = 2 6

T H = 764,62   ° R

Da equação ideal do gás, temos que:

P m í n V m á x = m R T L

A massa será:

m = P m í n V m á x R T L

Substituindo os dados, temos que:

m = 10 ⋅ 0,5 0,3704 ⋅ 510

m = 0,026   l b m

Passo 4

A partir da equação do gás ideal, também podemos encontrar a pressão máxima:

P m á x V m í n = m R T H

P m á x = m R T H V m í n

Substituindo os dados, temos que:

P m á x = 0,026 ⋅ 0,3704 ⋅ 764,62 0,06

P m á x = 122,72   p s i a

Resposta

T H = 764,62   ° R

m = 0,026   l b m

P m á x = 122,72   p s i a

Ver Outros Exercícios desse livro