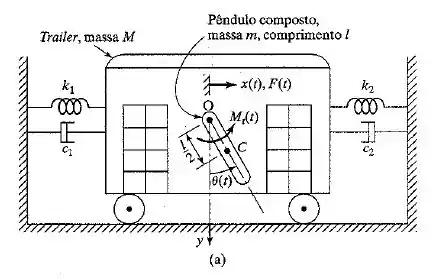
O coeficiente de influência inverso é definido como a velocidade induzida no ponto provocada por um impulso unitário aplicado no ponto . Utilizando essa definição, deduza a matriz de massa inversa do sistema mostrado na Figura 6.4(a).
Passo 1
Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto?
Primeiro, vamos combinar que indicam as coordenadas pra definir as posições linear e angular do móvel M e do pêndulo m, respectivamente. Pra gente derivar os coeficientes de influência de inércia inversa, primeiro nós vamos aplicar um impulso unitário linear no ponto 0, ao longo de e escreveremos as relações de momento-impulso observando a seguinte ilustração:
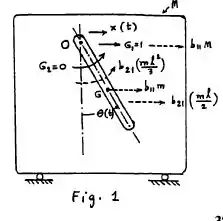
Assim, a relação de impulso-momento, ao longo de , se dá por:
Já a relação de impulso-momento ao longo de , se dá por:
Essas duas últimas equações combinadas, nos levam as seguintes conclusões, galera:
Passo 2
Agora, pessoal, vamos aplicar o impulso angular unitário no ponto 0(ao longo de ) e escrevemos as relações de impulso-momento observando agora a seguinte figura:
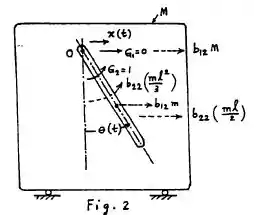
Assim, a relação de impulso-momento, ao longo de , se dá por:
Já a relação de impulso-momento ao longo de , se dá por:
Essas duas últimas equações combinadas, nos levam as seguintes conclusões, galera:
E finalmente, podemos montar a matriz de massa inversa já que já possuímos os componentes, teremos: