Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 15.Problemas - Ex. 109
A combustão de um combustível em geral resulta em um aumento da pressão quando o volume é mantido constante, ou em um aumento do volume quando a pressão é mantida constante, por conta do aumento do número de mols e da temperatura. O aumento da pressão ou do volume será máximo quando a combustão for completa e ocorrer adiabaticamente com a quantidade teórica de ar.Considere a combustão do vapor de álcool metílico ((g)) com a quantidade estequiométrica de ar em uma câmara de combustão de 1,5 L. Inicialmente, a mistura está a 25 °C e 101 kPa. Determine (a) a pressão máxima que pode ocorrer na câmara de
combustão, se a combustão ocorrer a um volume constante e (b) o volume máximo da câmara de combustão, se a combustão ocorrer a uma pressão constante.
Passo 1
Entendendo o problema:
Vapor de álcool metílico ) é queimado , e a combustão ocorre em proporções estequiométricas, ou seja, não há excesso de ar e a combustão é completa. A equação de combustão para o sistema é dada por:
Sendo o coeficiente a determinado por um balanço de massa na equação para o :
Então a equação de combustão é :
Passo 2
(item a):
A combustão ocorre em um sistema fechado, sob condições adiabática e sem interações por trabalho. Logo, e e o balanço de energia para esse tipo de sistema é:
(1)
Uma vez que os gases do sistema são admitidos como ideais, os termos V podem ser substituídos por RT. Logo:
(2)
A Figura 1 mostra a tabela com os respectivos valores de entalpia de formação e entalpia no estado padrão dos compostos da equação de combustão.
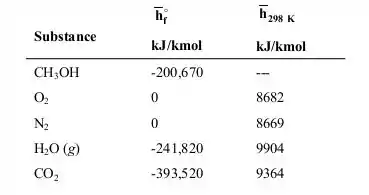
Figura 1: entalpia de formação e entalpia no estado padrão dos compostos da equação de combustão.
Uma vez que os reagentes estão no estado padrão e a entalpia de formação das substâncias simples é zero, a equação (2) aplicada a equação de combustão juntamente com os dados da Figura 1 torna-se:
=(1) (-200,67 – 8,314 . 298) + 1,5(0 – 8,314 . 298) + (5,64) (0 – 8,314 . 298)
Que leva a relação entre as entalpias:
Resolvendo (3) pelo método de tentativa e erro, sugerindo temperaturas, substituindo as entalpias correspondentes às temperaturas, o valor da temperatura que melhor ajusta a equação é
Como todos os gases reagentes e produtos são considerados ideais, a pressão máxima na câmara de combustão pode ser dada pela relação:
Com V sendo o volume constante, a pressão da entrada e o número de mols dos reagentes. é a temperatura de entrada dos reagentes. o número de mols dos produtos. E é a temperatura de chama calculada acima. Assim:
Passo 3
(item b):
A diferença deste caso para o item a, é que este ocorre a pressão constante. Nesse caso, o balanço de energia é o mesmo para os casos em regime permanente. Assim:
Como o processo é adiabático, com os reagentes no estado padrão:
Da tabela do item a e considerando entalpia nula de formação das substâncias simples, a aplicação da equação (4) juntamente com os dados da Figura 1 torna-se :
Que leva a:
Usando o mesmo procedimento do item a, de tentativa e erro, a temperatura obtida é
Da mesma maneira que o item a, considerando os gases ideais e agora a pressão constante, o volume máximo é:
Resposta
Ei, a resposta está no passo a passo :)