Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 68
Qual componente do ciclo de Rankine regenerativo ideal do Prob. 10-49E que perde a maior quantidade de potencial de trabalho? Considere que esse ciclo rejeita calor para um rio, cuja temperatura está a 60 °F e a fonte está a 800 °F.
Passo 1
Tá legal! A primeira coisa que vamos fazer é ilustrar o ciclo Rankine ideal com aquecedor de alimentação aberto e o seu diagrama T-s com a figura a seguir fornecida nessa seção do livro:
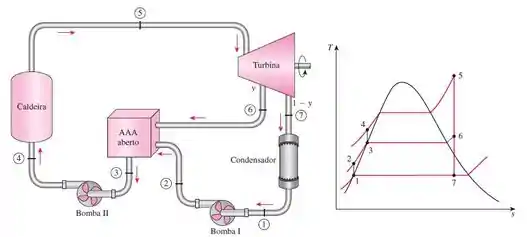
Primeiro temos que converter os dados fornecidos para podermos obter os dados nas tabelas termodinâmicas:
Tá legal! Agora vamos pegar os dados nas tabelas termodinâmicas referentes aos pontos que temos informações, então, temos:
Passo 2
Com os dados coletados até agora, podemos calcular o trabalho específico da bomba 1, então, temos:
Substituindo os valores conhecidos, temos:
Agora então podemos aplicar o equilíbrio de energia específica para a bomba 1 para descobrir o valor da entalpia em 2, de modo que teremos:
Substituindo os valores conhecidos, temos:
Agora, da mesma forma, vamos calcular o trabalho específico da bomba 2:
Substituindo os valores conhecidos, temos:
E, com isso, agora, podemos encontrar a entalpia no ponto 4 aplicando o equilíbrio de energia específico para ela:
Substituindo os valores conhecidos:
Agora faltam os dados referentes aos pontos 6 e 7, dessa forma, sabendo que a expansão na turbina é isentrópica, temos , então, para o ponto 6, teremos:
Para a pressão , pegando os dados de interesse na tabela, temos:
Dessa forma, a entalpia no ponto 6 será:
Da mesma forma, para o ponto 7 a , temos:
E a entalpia nesse ponto será:
E, da mesma forma, para a entropia, temos:
Passo 3
Agora aplicando o balanço de energia para o regenerador, temos:
Como temos regime permanente, então a energia que entra é igual a energia que sai, então:
Sabendo que não temos calor ou trabalho entrando ou saindo do sistema e que podemos desprezar as variações de energia cinética e potencial, dessa forma a equação do balanço de energia se torna:
De acordo com a proporção mássica ilustrada no diagrama do passo 1, podemos reescrever a equação como:
Substituindo os valores conhecidos, temos:
Agora, o calor rejeitado no condensador pode ser encontrado aplicando um equilíbrio de energia específica para o mesmo, então, teremos:
Substituindo os valores conhecidos, temos:
Agora precisamos encontrar o calor que entra no sistema pela caldeira, aplicando um balanço de energia específica na caldeira, temos:
Substituindo os valores conhecidos, temos:
Passo 4
Agora, sabendo que a equação da exergia específica destruída é dada por:
Em que a geração de entropia é dada por:
Então, a equação da exergia destruída se torna:
Então, aplicando a equação para o processo 4-5 temos:
Então, substituindo os valores conhecidos, temos:
Por fim, para o processo 7-1 do condensador, temos:
Então, substituindo os valores conhecidos, temos:
Agora, analisando o aquecedor de água, sabemos que não há calor entrando ou saindo do sistema, somente variação de entropia, então, a equação da exergia destruída se torna:
Substituindo os valores conhecidos, temos:
E, para os processos 1-2, 3-4, 5-6 e 6-7, como são processos isoentrópicos, não temos entropia sendo gerada e consequentemente não temos exergia sendo destruída. Então, o componente que perde a maior quantidade de potencial de trabalho é a caldeira, processo 4-5.