Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 53
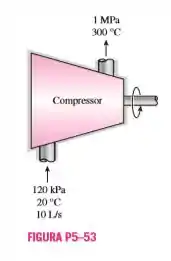
Um compressor de ar adiabático comprime 10 L/s de ar a 120 kPa e 20 °C para 1000 kPa e 300 °C. Determine (a) o trabalho requerido pelo compressor, em kJ/kg, e (b) a potência necessária para fazer o compressor de ar funcionar, em kW.
Passo 1
Temos que o balanço de energia pode ser dado por:
Adotando o compressor como sistema, temos as seguintes considerações:
- O compressor opera em regime permanente, ;
- O compressor é adiabático, ;
- As variações de altura e velocidades entre as correntes são desprezíveis, ;
Assim, o balanço de energia do compressor fica da seguinte maneira:
Passo 2
Temos que a variação de entalpia específica , pode ser dada por:
Como queremos saber o trabalho requerido pelo compressor por unidade de massa, vamos “embutir” o fluxo mássico dentro da variação de entalpia, assim:
Em tabelas, temos que o do ar é de 1,018 kJ/kgK. Convertendo as temperaturas para Kelvin, temos que e , substituindo na expressão, temos:
Passo 3
Temos que o fluxo mássico é dado por:
Porém, não nos foi fornecido o volume especifico, mas podemos calcula-lo da seguinte maneira:
Daí, teremos que o fluxo mássico é de
Passo 4
Temos pelo balanço de energia que, a potência utilizada para o compressor operar é de:
Resposta
Assim,
- O trabalho requerido pelo compressor é de 285,04 kJ/kg.
- A potência necessária para o compressor operar é de 4,065 kW.