Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 106

Um computador resfriado por um ventilador contém oito

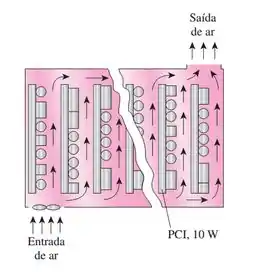
placas de circuito impresso (PCI). Cada uma dissipa potência equivalente a 10 W. As PCIs têm altura de 12 cm e comprimento de 18 cm. O ar de resfriamento é fornecido por um ventilador de 25 W montado na entrada. Considerando que o aumento da temperatura

do ar à medida que ele escoa pelo gabinete do computador não deve exceder 10 °C, determine (a) o fluxo de massa de ar que o ventilador precisa fornecer e (b) a fração da elevação de temperatura do ar decorrente do calor gerado pelo ventilador e por seu motor.

Passo 1

Vamos começar a questão assumindo algumas coisas:

  1. O sistema está operando em regime permanente
  2. As diferenças de energia potencial e cinética são desprezíveis
  3. A pressão atmosférica local é 1   a t m = 101,325   k P A

Propriedades:

O calor específico do ar para a temperatura ambiente é C p = 1,005   k J / k g . º C da tabela A - 2 da página 909.

Passo 2

Calculando a quantidade de calor dissipada pela placa de circuito completa:

Q ˙ T = N × Q ˙

O número de PCI’s num computador é N e a quantidade de calor dissipada por cada PCB é Q ˙

Q ˙ T = 8 × 10 Q ˙ T = 80   W

Passo 3

Escrevendo o balanço de massa:

m ˙ e n t r a d a = m ˙ s a í d a = m ˙ a r

O balanço de energia para a conservação energética é dado por:

E ˙ e n t r a d a = E ˙ s a í d a

Como as evariações de energia potencial e cinética são desprezíveis, podemos escrever:

Q ˙ T + m ˙ e n t r a d a h e n t r a d a = m ˙ s a í d a h s a í d a + W ˙

Em que apotência fornecida pelo ventilador é W ˙

Substituindo m ˙ a r por m ˙ e n t r a d a e m ˙ s a í d a :

Q ˙ T = m a r h s a í d a - h e n t r a d a + W ˙

Sabendo que h = C p T :

Q ˙ T = m ˙ a r C p a r T s a í d a - C p a r T e n t r a d a + W ˙ Q ˙ T = m ˙ a r C p a r T s a í d a - T e n t r a d a + W ˙

Substituindo Q T ˙ = 80 W , C p a r = 1,005 × 10 3   J / k g º C , T s a í d a - T e n t r a d a = 10 º C e W ˙ = - 25 W

80 = m ˙ a r × 1,005 × 10 3 × 10 + - 25 m ˙ a r = 0,0104   k g / s

Portanto o fluxo de massa de ar que o ventilador precisa fornecer é 0,0104   k g / s

Passo 4

b) Calculando a diferença de temperatura

W ˙ = m ˙ a r × C p × Δ T

Substituindo W ˙ = 25   W , C p a r = 1,005 × 10 3   J / k g º C e m ˙ a r = 0,0104   k g / s

25 = 0,0104 × 1005 Δ T Δ T = 2,391 º Δ T ≈ 2,4 º C

Finalmente, calculando a fração da elevação da temperatura:

f = Δ T 2 Δ T 1 × 100 %

Substituindo Δ T 2 = 2,4 º e Δ T 1 = 10 º C

f = 2,4 10 × 100 % = 24 %  

Portanto, a fração de elevação da temperatura é 24%

Resposta

a ) m ˙ a r = 0,0104   k g / s b ) f = 24 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o circuito equivalente para uma ligação em paralelo de capacitores ideais. Suponha que a tensão inicial nos capacitores em paralelo seja v(t0). (Sugestão: some as correntes dos capacitores r
No circuito da Figura 5.12, o amp op é ideal. Dado que Ra = 4 kV, Rb = 5 kV, Rc = 20 kV, va = 200 mV, vb = 150 mV, vc = 400 mV e VCC = ;6 V, especifique a faixa de variação de Rf para a qual o amp op
Determine o circuito equivalente para uma ligação em paralelo de capacitores ideais. Suponha que a tensão inicial nos capacitores em paralelo seja v(t0). (Sugestão: some as correntes dos capacitores r
a) Partindo da Equação 6.59, mostre que o coeficiente de acoplamento também pode ser expresso comob) Com base nas frações 21/1 e 12/ 2, explique por que k é menor do que 1,0.
Repita o Problema 4.105 considerando que o valor de Ig2 aumente para 17 A e todos os outroscomponentes continuem com seus valores nominais. Verifique suas previsões usando uma ferramenta como PSpice o