Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 10.Problemas - Ex. 48
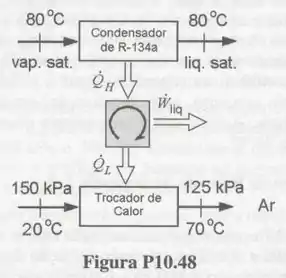
Um condensador de é utilizado como fonte térmica de um motor térmico cíclico que opera em regime permanente (veja a Fig. P10.48). O refrigerante entra no condensador como vapor saturado a e o deixa como líquido saturado a . A vazão em massa de no condensador é . A máquina térmica rejeita calor num trocador de calor resfriado a ar. O ar entra no trocador a e e o deixa a e . A taxa global de geração de irreversibilidade neste processo é igual a . Determine a vazão em massa de ar no trocador de calor e a eficiência térmica da máquina térmica.
Passo 1
Opa, tudo bem?
Preparado para resolver essa questão comigo?
Bora lá então!
Começamos o nosso problema expondo alguns dados do nosso sistema e obtendo algumas propriedades dos estágios do nosso processo pela Tabela B.5.1 para o :
Estágio 1:
Assim:
Estágio 2:
Assim:
Passo 2
Analisando o trocador de calor a ar:
Entrada:
Saída:
Calculando :
Passo 3
Sabendo que a geração de irreversibilidade é dada por:
Isolando :
Substituindo os dados:
Passo 4
Por fim, o problema nos pede a eficiência térmica da máquina térmica.
Aplicando a equação de energia em cada linha:
Com:
Isolando , temos
Para o :
Para o Ar:
Assim, temos que o trabalho líquido é dado por:
Por fim, calculando a eficiência:
E assim finalizamos a nossa questão.
Te espero na próxima!