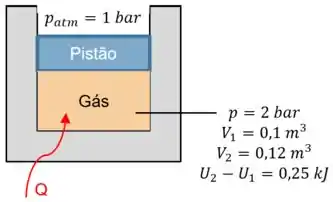
Conforme ilustrado na figura abaixo, um gás contido em um conjunto cilindro-pistão, inicialmente a um volume de 0,1 m³, passa por uma expansão a pressão constante de 2 bar até o volume final de 0,12 m³, enquanto é aquecido lentamente através da base. A variação de energia interna do gás é de 0,25 kJ. Considere que as paredes do pistão e do cilindro são fabricadas com um material resistente ao calor e que pistão se move lentamente no cilindro. A pressão atmosférica local é de 1 bar.
(a) Determine o trabalho e a transferência de calor, ambos em kJ, considerando o gás como o sistema.
(b) Determine o trabalho e a variação da energia potencial, ambos em kJ, considerando o pistão como o sistema.
Passo 1
Faaaala pessoal! Beleza? Vamos começar mais essa questão?
Primeiro vamos dar uma organizada nos dados aqui:
Vamos também levantar algumas hipóteses importantes para o cálculo:
1 – São considerados dois sistemas fechados, o gás e o pistão.
2 – O gás passa por um processo à pressão constante.
3 – Para o gás não há variação de energia potencial, nem de energia cinética.
4 – Para o pistão, não há transferência de calor. Também não há mudança em sua energia interna e energia cinética e não há atrito com as paredes.
Agora vamos para os cálculos!

Passo 2
Para a letra (a) vamos trabalhar apenas com o gás como mostra a seleção na imagem abaixo!
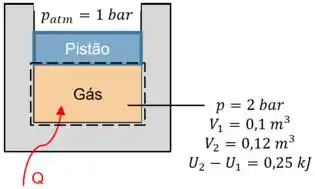
Do gás nós só temos informações sobre pressão e volume, certo?
Você lembra qual a fórmula do trabalho em relação a pressão e volume? É essa daqui, olha:
Lembra que no enunciado ele falou que a expansão que o gás sobre é à pressão constante? Podemos coloca essa pressão para fora da integral!
Opa! Nós já temos p, e ! Já podemos achar esse trabalho:
Que beleza! Agora vamos achar o calor através da aplicação da primeira lei da termodinâmica.
Dá uma relembrada lá na hipótese! O gás não sofre variação nem de energia potencial, nem de energia cinética! Então a variação de energia se dá apenas pela variação de energia interna.
Durante a questão já nos foi dada essa variação de energia interna! E acabamos de achar o trabalho W. Agora é só isolar o Q e substituir os dados. Molezinha né?
Agora já temos tanto o trabalho quanto o calor!!! Terminamos a letra (a)! Vamos só passar as unidades para kJ:
Bem tranquilo né? Vamos para a letra b!
Passo 3
Agora vamos tomar o pistão como sistema fechado para análise!
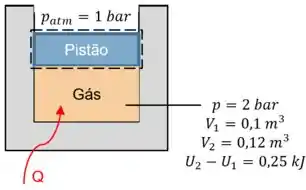
Vamos dar uma analisada... O que vai ocorrer com o pistão quando o gás se expande? Concorda que o gás vai apenas empurrar o pistão para cima? Então o trabalho desse sistema vai depender do deslocamento vertical do pistão!
Qual a fórmula do trabalho que envolve o deslocamento? A nossa velha conhecida:
Mas quem vai ser essa força? Ela é a força em relação às pressões que o pistão sofre! Vamos ter então:
Podemos reorganizar da seguinte maneira:
Se o é o deslocamento vertical do pistão, ou seja, o quanto o gás expandiu em altura, temos que será igual ao volume expadindo pelo gás! Então:
Voltando então para a equação do trabalho:
E já temos todos os dados para esse cálculo!
Agora vamos calcular a energia potencial envolvida através da primeira lei da termodinâmica!
Vamos lembrar da hipótese 4! Não há troca de calor, nem variação de energia cinética e interna no pistão! Então:
Show de bola!! Achamos tudo que a questão pediu, então terminamos por aqui! Vamos para a próxima questão.
Resposta
(a)
(b)