Enunciado
Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 48
A estrutura de uma parede isolada de uma casa possui condutividade térmica média de 0,04 Btu/h.ft.°R (0,07 W/m.K). A espessura de parede é de 6 in (0,15 m). A temperatura do ar interno é 70°F (21,1 °C), e o coeficiente de transferência de calor por convecção entre o ar interno e a parede é 2 Btu/h.ft².°R (11,4 W/m².K). No lado externo, a temperatura do ar ambiente é 32°F (0°C) e o coeficiente de transferência de calor por convecção entre a parede e o ar externo é 5 Btu/h.ft².°R (28,4 W/m².K). Determine a taxa de transferência de calor através da parede, em regime permanente, em Btu/h por ft² de área de superfície.
Passo 1
Fala galera!!! Tudo certinho? Vamos fazer mais uma questão de parede?
Vamos começar dando uma organizada nos dados:
Beleza! Mesmo assim não dá para entender nada né? Como é essa situação do enunciado? Vamos listar o que acontece no processo para ficar melhor de entender!
1 - O ar interno, que está mais quente que o ar externo, transfere calor para o lado da parede que está em contato com ele por convecção, sem perdas.
2 – O lado interno da parede, que acabou de receber o calor do ar interno, vai transferir esse mesmo calor para o lado externo da parede por condução. De forma que a temperatura varia de maneira linear e tudo em regime permanente, bem devagarzinho, sem perdas.
3 - Por fim, o lado externo da parede passa esse calor para o ar externo através também da convecção, sem perdas.
Ficando assim o esquema:
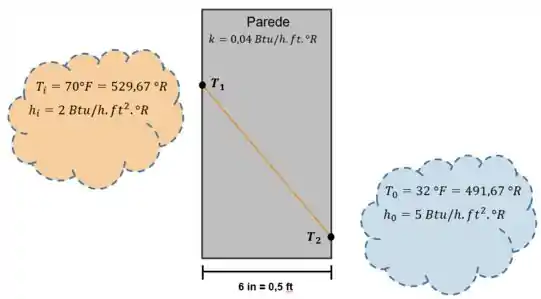
Show de bola! Agora vamos partir para as contas!
Passo 2
Lembra que ali no detalhamento do processo tudo foi falado que era sem perdas?
Então vamos ter que o calor transferido por convecção do ar interno para a parede é igual ao calor transferido por condução por dentro da parede que, por fim, é igual ao calor transferido por convecção para o ar externo!
Deve ser mais fácil de ver essa frase na forma de equação né?
Ou seja:
Ou melhor:
Dessas incógnitas do sistema, nós não temos , nem . E agora???
Passo 3
Vamos manter a calma! É só isolar na equação 1 do sistema e na equação 3 do sistema!
Mas vamos fazer uma coisa de cada vez.
Primeiro, vamos isolar na equação 1:
E agora vamos isolar o na equação 3:
Pronto! Agora já podemos eliminar o problema substituindo e na equação 2!
Passo 4
Lembra da equação 2?
Substituindo o e que achamos antes, ela fica assim:
Mas ficou bem feia né? Vamos dar uma organizada!
Falta só mais um pouquinho, tá bom? Só isolar o agora!
Por fim, só mais uma ajeitadinha! Prometo!!
Ufa! Até que enfim! Agora é só substituir e partir pro abraço!
Pronto!!! Conseguimos! Descansa um pouco e vamos para a próxima!