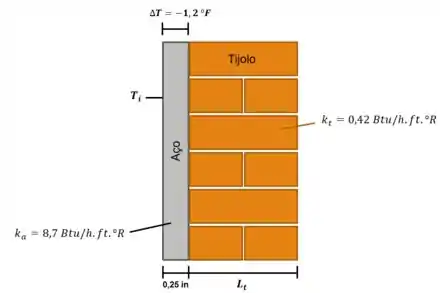
Conforme mostrado na figura abaixo, a parede externa de um forno é composta por uma camada de aço de 0,25 in (0,006 m) de espessura, sendo = 8,7 Btu/h.ft.°R (15,1 W/m.K) e uma camada de tijolos, sendo = 0,42 Btu/h.ft.°R (0,73 W/m.K). Em regime permanente ocorre um decréscimo de temperatura de 1,2 °F (0,7 °C) na camada de aço. A temperatura relativa à superfície exposta da camada de aço é 540 °F (282,2 °C). Se a temperatura da superfície externa do tijolo não pode ser maior do que 105 °F (40,6 °C), determine a espessura mínima de tijolo, em in, que assegura que esse limite seja alcançado.
Passo 1
Primeiro vamos considerar algumas hipóteses importantes:
1 – O processo na parede ocorre em regime permanente.
2 – A temperatura varia linearmente através de ambas paredes.
E agora vamos só dar uma reorganizada nos dados, lembrando da conversão de Fahrenheit para Rankine!
Passo 2
Primeiro, vamos achar a temperatura no contato entre as paredes .
Passo 3
Em ambas paredes o processo de transferência de calor ocorre por condução! Então:
Pela hipótese 1 e 2, temos:
Para o aço:
Para o tijolo:
Certo, agora podemos igualar a equação do aço à equação do tijolo, como dito lá em cima!
Já que queremos calcular o , vamos isolá-lo!
Passo 4
Nós queremos a espessura mínima de tijolo para que a temperatura do lado externo da parede de tijolos seja menor ou igual à 105 °F, certo?
Então:
Então a nossa equação passa a ser uma inequação:
Substituindo os dados: