O gás oxigênio () em um conjunto cilindro-pistão passa por uma expansão, indo de um volume até um volume = 0,03 m³. A relação entre a pressão e o volume durante o processo é em que A = 0,06 bar.m³ e B = 3,0 bar. Para o , determine (a) as pressões inicial e final, ambas em bar, e (b) o trabalho, em kJ.
Passo 1
Vamos começar dando uma analisada no enunciado. O esquema de um conjunto cilindro-pistão que contém o gás é o seguinte:
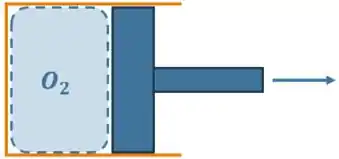
Foi dito que esse conjunto aí de cima respeita a relação . E também foram fornecidos alguns dados:
Assim temos a relação
Com isso tudo organizado, vamos para os próximos passos.
Passo 2
Na letra (a) ele nos pede as pressões inicial e final do sistema. Já que temos a relação entre pressão e volume, basta substituir os volumes para acharmos as pressões!
Para a situação inicial:
Para a situação final:
Tranquilo né? Vamos adiante!
Passo 3
Agora vem o cálculo do trabalho na letra (b):
Como
Podemos separar em duas integrais para facilitar a visualização:
Assim, continuamos com os cálculos:
Para passar de bar.m³ para kJ é só multiplicar por 100!
Resposta
a)
b) W = 12,59 kJ