Um conjunto cilindro –pistão contém de ar. Inicialmente, a temperatura e a pressão no ar são iguais a e . O ar é então aquecido em dois processos sucessivos. O primeiro processo corre a volume constante e a temperatura é elevada até atingir . Já o segundo processo ocorre a pressão constante e termina quando a temperatura do ar se torna igual a . Determine o volume do ar no estado final do segundo processo e o trabalho realizado nos dois processos.

Pessoal seguinte, para determinar o volume no estado 3 teremos que utilizar as relações de proporção do sistema cilindro pistão.

Como estamos nesse tipo de conjunto para o estado 2 indo para estado 3, temos a seguinte proporção:

Agora com essa proporção em mente fica fácil dizer qual variável falta, temos que determinar .

Para determinar vamos lembrar que e iremos considerar que o nosso ar é um gás ideal, com essa consideração vamos utilizara equação do gás ideal para determinar os volumes.

Olhando na tabela , temos que , substituindo valores na fórmula e isolando o volume, fica:

Com o volume determinado vamos calcular o volume no estado final:

Galera para determinar o trabalho realizado no processo total, temos que trabalho depende da variação do volume e da pressão de cada estado.

O único estado que não temos a pressão calculada ainda é o segundo, portanto, vamos utilizar outra regrinha de proporção devido o sistema.

Substituindo valores:

Para determinar o trabalho sabemos que ele é uma área integrável de um diagrama , por isto, vamos montar o diagrama do nosso problema:

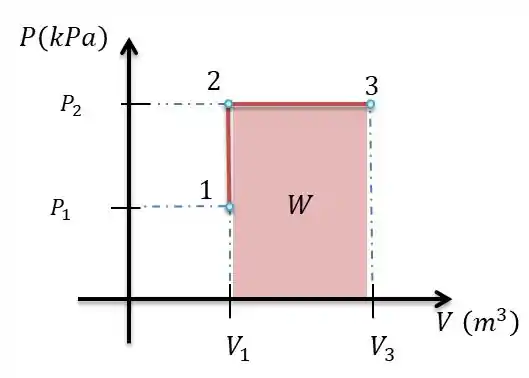
Como o trabalho se da pela área em baixo dos nossos processos, vamos calcular a área desse retângulo e teremos o nosso trabalho:

Lembrando que e , substituindo valores:

É fecho pessoal, valeu.