Exercícios de Trabalho de Movimento da Fronteira - Lista de Exercícios Resolvida

Um conjunto cilindro-pistão contém ar. Inicialmente, o ar está a , e o volume ocupado pelo ar é . Um processo a pressão constante é realizado e detecta-se o fornecimento de de trabalho. Determine o volume e a temperatura no estado final desse processo.

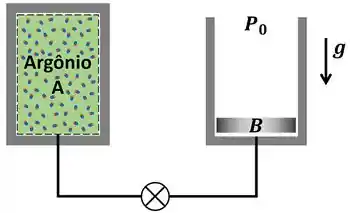
Um tanque de , (veja Figura), contém gás argônio a e . O cilindro , com um pistão que se movimenta sem atrito e massa tal que flutua com uma pressão interna de , está inicialmente vazio. A válvula que liga os dois recipientes é, então, aberta e o argônio escoa para e atinge um estado uniforme a e . Qual o trabalho realizado pelo argônio durante esse processo?

Uma amostra de gás Hélio expande do estado inicial (, e ) até o estado final onde . Sabendo que a expansão é politrópica com , determine o trabalho realizado no processo.

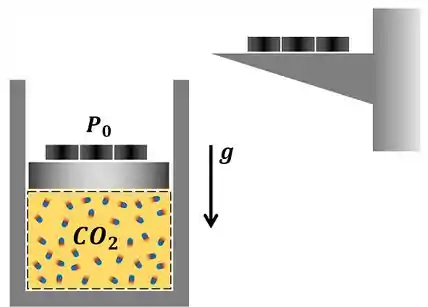
O conjunto cilindro-pistão mostrado na figura abaixo contém, inicialmente de dióxido de carbono a e . Os pesos são, então, adicionados a uma velocidade tal que o gás é comprimido segundo a relação . Admitindo que a temperatura final seja igual a , determine o trabalho realizado nesse processo.

de um gás perfeito a contido em um cilindro-pistão expande isobaricamente, provocando uma variação de no seu volume. Considerando que este gás ocupava antes da sua expansão, determine o trabalho realizado pelo gás em joule.

Um gás contido em um cilindro-pistão expande isobaricamente, provocando uma variação de no seu volume. Considerando que este gás é mantido a no interior do cilindro, determine o trabalho realizado pelo gás em joule.

Uma amostra de ar é comprimida do estado inicial ( e ) até o estado final onde a temperatura é igual a e a pressão é igual a . Sabendo que a compressão é politrópica, determine o expoente relativo ao processo e o trabalho específico associado ao processo. Considere a massa molar do ar igual a .

Um conjunto cilindro-pistão contém, inicialmente, de um gás a e . O gás é então expandido num processo onde . Admitindo que a pressão final seja igual a , determine o trabalho envolvido no processo.